Hierarchical Models

Objectives

  • General Use and Language
  • Examples
  • Case studies
    • random intercept
    • random intercept & slope
  • Considerations

Names

  • multilevel model
  • mixed model
  • random effects model
  • nested data model
  • split-plot model

Sort of definitions

  • models where parameters vary at more than one level
  • models in which lower levels are sorted under a hierarchy of successive higher-level units
  • Generalization of linear and generalized linear modeling in which regression coefficients are themselves given a model whose parameters are also estimated from data (Gelman)
  • Model where unobserved parameters are estimated as a function of other unobserved parameters

Hobbs and Hooten 2015 (pg. 109)

  • Representing variation among individuals arising, for example, from genetics, location, or experience.

  • Studying phenomena operating at more than one spatial scale or level of ecological organization.

  • Modeling a process as well as uncertainty that results from imperfect observations of the process.

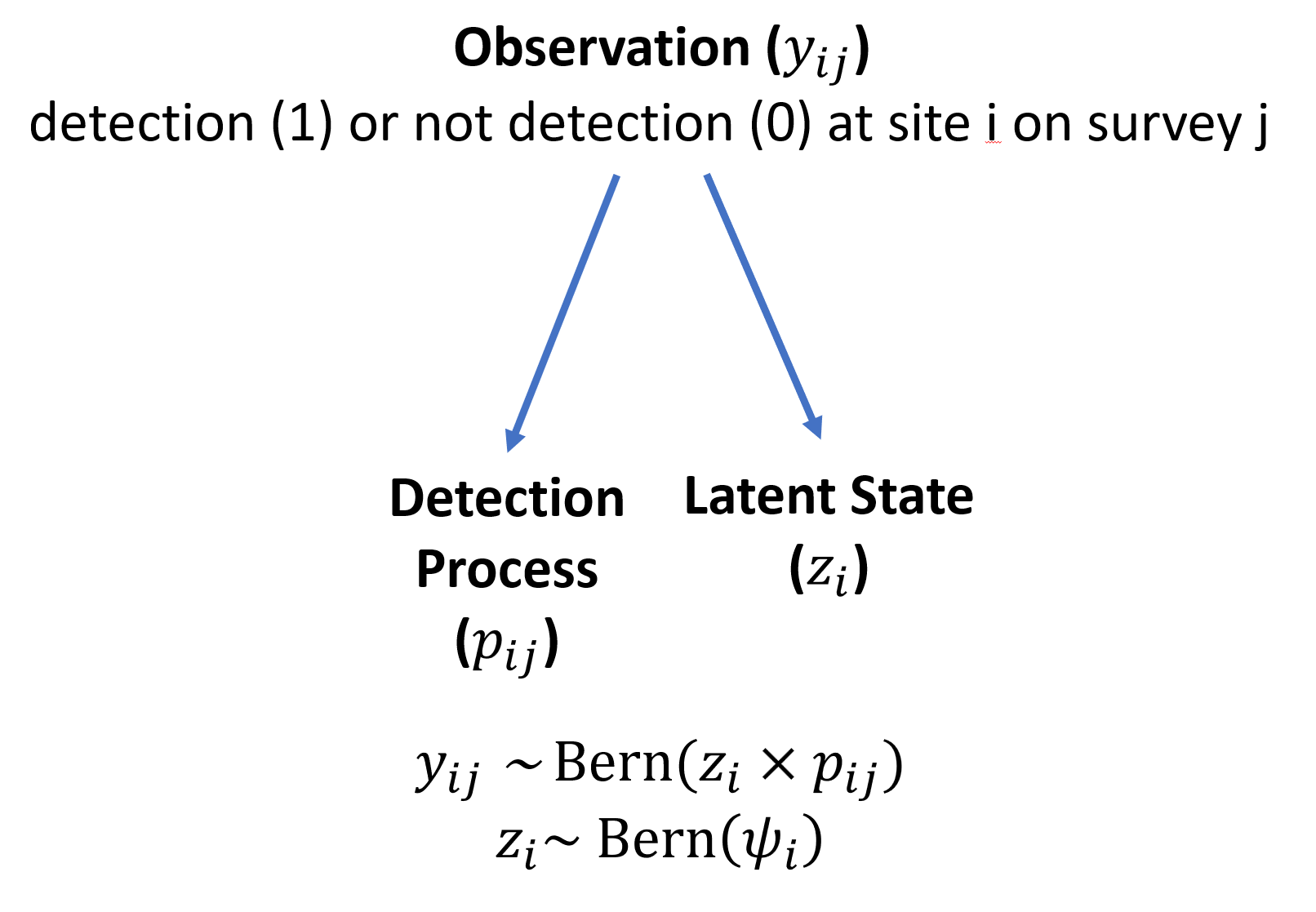
  • Understanding changes in states of ecological systems that cannot be observed directly. These states arise from “hidden” processes.

General Types

  • Random Effect / Multi-level Model

  • latent/unobserved state or process

Random Effect

Andrew Gelman Blog Post

Paper Link

“People are always asking me if I want to use a fixed or random effects model for this or that.”


“I always reply that these terms have no agreed-upon definition.”


“People with their own favorite definitions don’t always realize that other definitions are out there. Worse, people conflate different definitions”.

Example 1

  • student grades within classroom, within school

Example 2

  • forest cover effect on occurrence of bobcats at different protected areas

Random Effect / Multi-level Model

  • repeated measurements of individual within population

  • repeated measurements at a small spatial scale that is part of a larger one

Hierarchical Structure to Data

Hierarchical Structure to Data

Hierarchical Structure to Data

Hierarchical Structure to Data

Hierarchical Structure Example

Study goals

  • Estimate state-wide average mass

  • Understand site-level variation

Hierarchical Structure Example

Complete Pooling

  • Ignores variance across sites, which is a goal of study
  • Data within sampling site might not be independent, leading to pseudoreplication (depressed variance)

No Pooling

  • No state-level estimate
  • Estimator for each site may be biased, particularly at low sample sizes

Partial Pooling (Hierarhical Model)

Latent State






Case Study

Data and Problem

We sample Amur Leopards in five different vegetation types of Land of the Leopard National Park.

Interested in detection rate by vegetation type and overall.

Data and Problem

We sample Amur Leopards in five different vegetation types of Land of the Leopard National Park.

Detection Rate = Independent Counts / Effort

Data

   y  veg effort
1 15 Veg1      5
2 18 Veg1      5
3 12 Veg2      5
4 14 Veg2      5
5 12 Veg2      5
6 14 Veg2      5

Veg1 Veg2 Veg3 Veg4 Veg5 
   2   20   20   10   10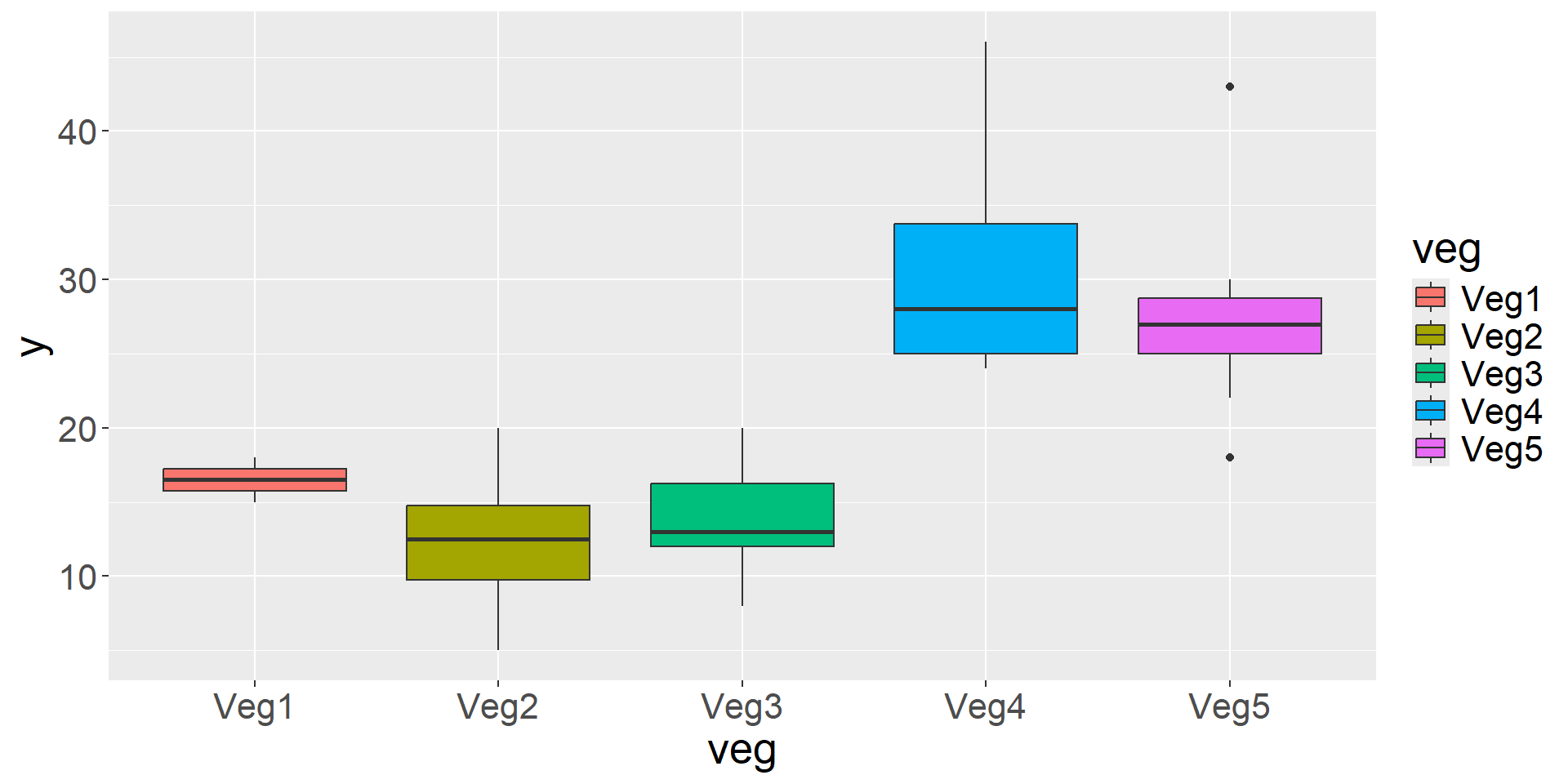

Model 1 (Complete Pooling)

library(glmmTMB)
library(broom.mixed)

model1 = glmmTMB(y~1, family=poisson(link="log"),data=dat)


summary(model1)
 Family: poisson  ( log )
Formula:          y ~ 1
Data: dat

     AIC      BIC   logLik deviance df.resid 
   532.2    534.4   -265.1    530.2       61 


Conditional model:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)  2.91165    0.02962   98.31   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Model 1 (Complete Pooling)

marginaleffects::predictions(model1,type = "response")

 Estimate Std. Error    z Pr(>|z|)     S 2.5 % 97.5 %
     18.4      0.545 33.8   <0.001 827.7  17.3   19.5
     18.4      0.545 33.8   <0.001 827.7  17.3   19.5
     18.4      0.545 33.8   <0.001 827.7  17.3   19.5
     18.4      0.545 33.8   <0.001 827.7  17.3   19.5
     18.4      0.545 33.8   <0.001 827.7  17.3   19.5
--- 52 rows omitted. See ?avg_predictions and ?print.marginaleffects --- 
     18.4      0.545 33.8   <0.001 827.7  17.3   19.5
     18.4      0.545 33.8   <0.001 827.7  17.3   19.5
     18.4      0.545 33.8   <0.001 827.7  17.3   19.5
     18.4      0.545 33.8   <0.001 827.7  17.3   19.5
     18.4      0.545 33.8   <0.001 827.7  17.3   19.5
Columns: rowid, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high, y 
Type:  response

Model 2 (No Pooling)

model2 = glmmTMB(y~veg, family=poisson(link="log"),data=dat,
                 contrasts = list(veg = "contr.sum"))
summary(model2)
 Family: poisson  ( log )
Formula:          y ~ veg
Data: dat

     AIC      BIC   logLik deviance df.resid 
   369.4    380.1   -179.7    359.4       57 


Conditional model:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)  2.93764    0.04235   69.37  < 2e-16 ***
veg1        -0.13427    0.14133   -0.95    0.342    
veg2        -0.42398    0.06498   -6.52 6.82e-11 ***
veg3        -0.29146    0.06262   -4.65 3.25e-06 ***
veg4         0.47681    0.06138    7.77 7.94e-15 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Model 2 (No Pooling)

marginaleffects::predictions(model2, 
                             newdata = data.frame(veg=c("Veg1","Veg2","Veg3","Veg4","Veg5")),
                             re.form=NA)

 Estimate Std. Error     z Pr(>|z|)     S 2.5 % 97.5 %
     16.5      2.872  5.74   <0.001  26.7  10.9   22.1
     12.4      0.786 15.72   <0.001 182.5  10.8   13.9
     14.1      0.840 16.79   <0.001 207.8  12.5   15.7
     30.4      1.744 17.44   <0.001 223.7  27.0   33.8
     27.4      1.655 16.55   <0.001 202.0  24.2   30.6

Columns: rowid, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high, veg, y 
Type:  response

Model 3 (Partial Pooling)

model3 = glmmTMB(y~1+(1|veg), family=poisson(link="log"),data=dat)
summary(model3)
 Family: poisson  ( log )
Formula:          y ~ 1 + (1 | veg)
Data: dat

     AIC      BIC   logLik deviance df.resid 
   384.4    388.6   -190.2    380.4       60 

Random effects:

Conditional model:
 Groups Name        Variance Std.Dev.
 veg    (Intercept) 0.1299   0.3604  
Number of obs: 62, groups:  veg, 5

Conditional model:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)   2.9391     0.1662   17.69   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Model 3 (Partial Pooling)

ranef(model3)
$veg
     (Intercept)
Veg1  -0.1103110
Veg2  -0.4126484
Veg3  -0.2851561
Veg4   0.4635429
Veg5   0.3612502


broom.mixed::tidy(model3, effects = "ran_vals", conf.int = TRUE)
# A tibble: 5 × 9
  effect   component group level term      estimate std.error conf.low conf.high
  <chr>    <chr>     <chr> <chr> <chr>        <dbl>     <dbl>    <dbl>     <dbl>
1 ran_vals cond      veg   Veg1  (Interce…   -0.110     0.206  -0.514     0.294 
2 ran_vals cond      veg   Veg2  (Interce…   -0.413     0.173  -0.751    -0.0738
3 ran_vals cond      veg   Veg3  (Interce…   -0.285     0.172  -0.622     0.0520
4 ran_vals cond      veg   Veg4  (Interce…    0.464     0.172   0.126     0.801 
5 ran_vals cond      veg   Veg5  (Interce…    0.361     0.173   0.0230    0.699 


confint(model3, component = c("all"))
                            2.5 %    97.5 %  Estimate
(Intercept)             2.6134002 3.2647754 2.9390878
Std.Dev.(Intercept)|veg 0.1896794 0.6846043 0.3603545



fixef(model3)

Conditional model:
(Intercept)  
      2.939  


#Predictions - does not include RE uncertainty
preds = predict(model3,
                newdata=data.frame(veg=c("Veg1","Veg2","Veg3","Veg4","Veg5")),
                type="link",
                re.form=NULL,
                se.fit = TRUE
                )


preds$LCL = exp(preds$fit-1.96*preds$se.fit)
preds$UCL = exp(preds$fit+1.96*preds$se.fit)
preds$fit = exp(preds$fit)

data.frame(preds)
       fit     se.fit      LCL      UCL
1 16.92475 0.15877885 12.39843 23.10348
2 12.50889 0.06300056 11.05583 14.15291
3 14.20980 0.05890828 12.66030 15.94893
4 30.04303 0.05761047 26.83519 33.63433
5 27.12181 0.06039730 24.09392 30.53021


#A typical site (non an average site)
# Done by setting the random effect mean to 0
predict(model3,type="response",re.form=NA)[1]
[1] 18.8986

Model 3b

library(lme4)
model3b = glmer(y~1+(1|veg), family=poisson(link="log"),data=dat)
equatiomatic::extract_eq(model3b)

\[ \begin{aligned} \operatorname{y}_{i} &\sim \operatorname{Poisson}(\lambda_i) \\ \log(\lambda_i) &=\alpha_{j[i]} \\ \alpha_{j} &\sim N \left(\mu_{\alpha_{j}}, \sigma^2_{\alpha_{j}} \right) \text{, for veg j = 1,} \dots \text{,J} \end{aligned} \]

Alt Model Notation

\[\begin{align*} y_{i} \sim& \text{Poisson}(\lambda_{i})\\ \text{log}(\lambda_{i}) =& \mu + \alpha_{j[i]}\\ \alpha_{j} \sim& \text{Normal}(0, \sigma^2_{\alpha}) \end{align*}\]

Pooling Information

Pooling Information

Pooling Information

Random Intercept + Slope

Leopard detection varies by cover and veg, where the effect of cover comes from a shared distribution

  y         cov  veg
1 3  0.40161608 Veg1
2 0 -0.12360373 Veg1
3 3  0.62883136 Veg1
4 0  0.07607150 Veg1
5 2  0.04150764 Veg1
6 0 -0.39289231 Veg1

Random Intercept + Slope

re.model = glmer(y~cov+(cov|veg), family=poisson(link="log"),data=dat2)
summary(re.model)
Generalized linear mixed model fit by maximum likelihood (Laplace
  Approximation) [glmerMod]
 Family: poisson  ( log )
Formula: y ~ cov + (cov | veg)
   Data: dat2

     AIC      BIC   logLik deviance df.resid 
 14274.7  14295.8  -7132.4  14264.7      495 

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
 -4.798  -2.443  -1.630  -0.946 145.188 

Random effects:
 Groups Name        Variance Std.Dev. Corr
 veg    (Intercept) 0.4896   0.6997       
        cov         0.1392   0.3732   0.14
Number of obs: 500, groups:  veg, 5

Fixed effects:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)   1.6210     0.3137   5.166 2.39e-07 ***
cov           0.1121     0.1683   0.666    0.505    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
    (Intr)
cov 0.140

Random Intercept + Slope

  • Called conditional mean predictions
marginaleffects::plot_predictions(re.model, condition=c("cov","veg"),
                                  type="link", re.form=NULL)

Random Intercept + Slope

marginaleffects::plot_predictions(re.model, condition=c("cov","veg"),
                                  type="link", re.form=NA)

Random Intercept + Slope

equatiomatic::extract_eq(re.model)

\[ \begin{aligned} \operatorname{y}_{i} &\sim \operatorname{Poisson}(\lambda_i) \\ \log(\lambda_i) &=\alpha_{j[i]} + \beta_{1j[i]}(\operatorname{cov}) \\ \left( \begin{array}{c} \begin{aligned} &\alpha_{j} \\ &\beta_{1j} \end{aligned} \end{array} \right) &\sim N \left( \left( \begin{array}{c} \begin{aligned} &\mu_{\alpha_{j}} \\ &\mu_{\beta_{1j}} \end{aligned} \end{array} \right) , \left( \begin{array}{cc} \sigma^2_{\alpha_{j}} & \rho_{\alpha_{j}\beta_{1j}} \\ \rho_{\beta_{1j}\alpha_{j}} & \sigma^2_{\beta_{1j}} \end{array} \right) \right) \text{, for veg j = 1,} \dots \text{,J} \end{aligned} \]

FAQ

GLMM FAQ

  • model specifications

  • predictions with uncertainty

  • Testing RE’s

Considerations

  • Shrinkage/Regularization

  • When to use a random effect?

Lab