Generalized Linear Models II
Objectives
- Poisson Regression
- Numerical Optimization
- Categorical variables >2 levels
- Effect Coding
- Variable Combinations
Pika Study

We sample plots of high elevation rocky outcrops, counting the number of American Pika within each plot; plot sizes are the same size.
Poisson Regression
We model the counts of American pika (\(y_{i}\)) at each site \(i = 1...n\) as a Poisson random variable with parameter \(\lambda\) being a function of our \(p\) site-level variables in \(n\) x \(p\) design matrix (\(\textbf{X}\)) and coefficients \(\boldsymbol{\beta}\) as,
\[ \begin{align*} \textbf{y} \sim & \text{Poisson}(\boldsymbol{\lambda})\\ \text{log}(\boldsymbol{\lambda}) =& \textbf{X}\boldsymbol{\beta}\\ \boldsymbol{\lambda} =& e^{\textbf{X}\boldsymbol{\beta}}. \end{align*} \]
Data
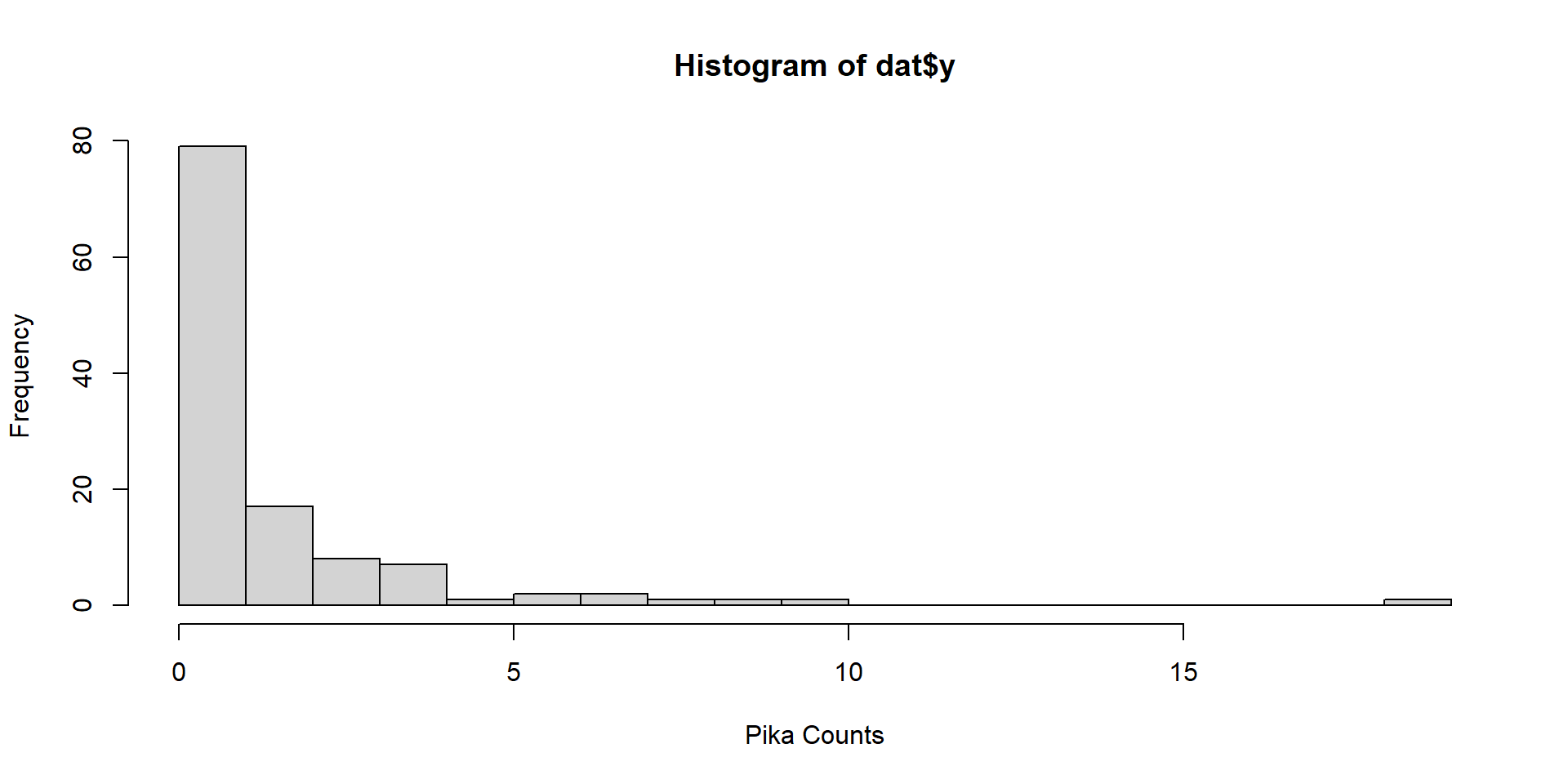
Counts by Site
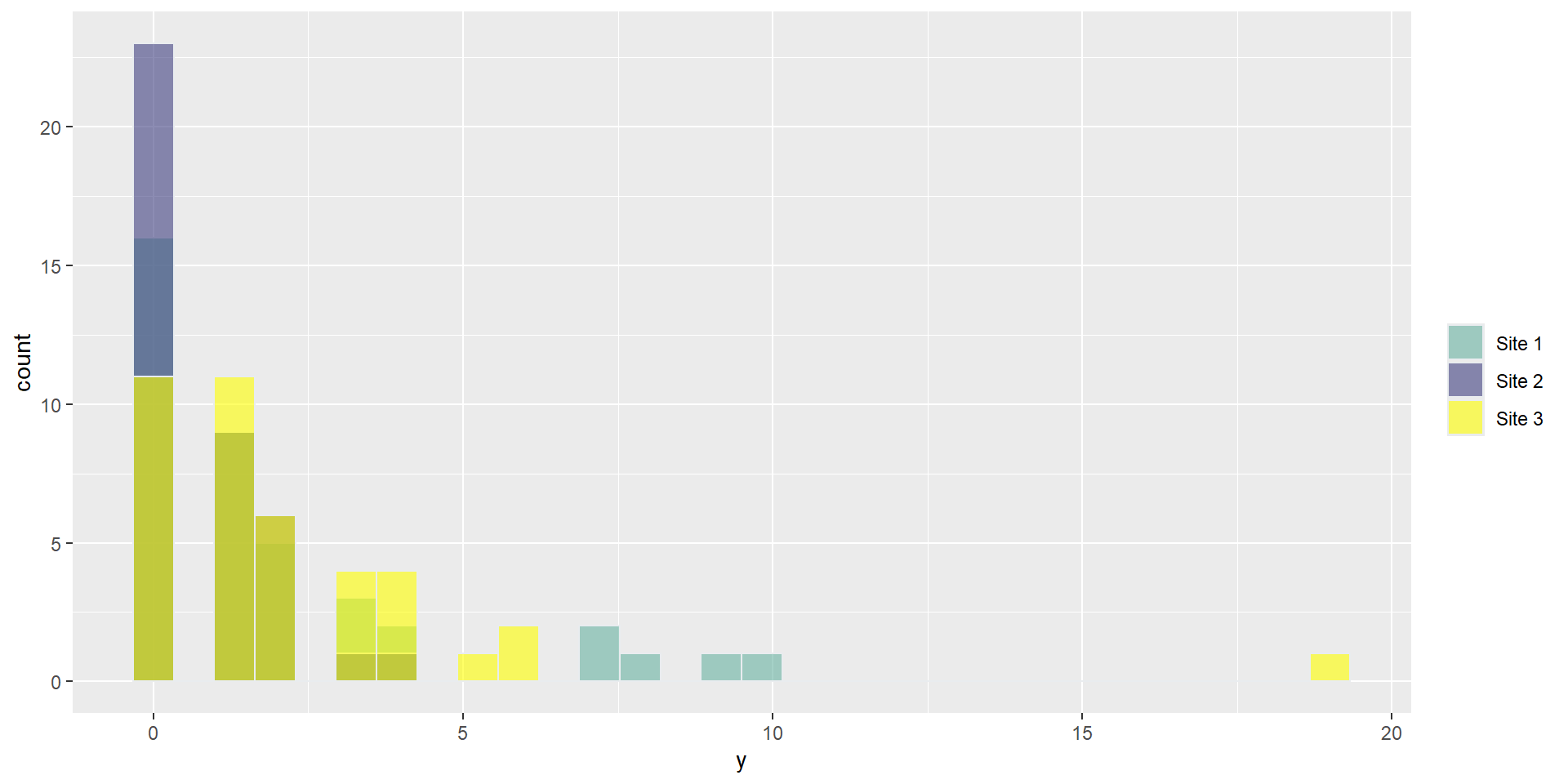
Fit Model
Interpret the Coefficients
Call:
glm(formula = y ~ site, family = poisson(link = "log"), data = dat)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.6549 0.1140 5.747 9.09e-09 ***
siteSite 2 -1.0116 0.2207 -4.584 4.56e-06 ***
siteSite 3 0.1221 0.1565 0.780 0.435
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 341.36 on 119 degrees of freedom
Residual deviance: 305.76 on 117 degrees of freedom
AIC: 496.33
Number of Fisher Scoring iterations: 6Numerical Optimization of Likelihood
Side-Bar
Negative Log-Likelihood Function
#Here is our negative log-likelihood function with three
#parameters - beta0, beta1, and beta2 (1)
#inputs = design matrix X
neg.log.like = function(par,X) {
#linear model of parameters par and design matrix (X)
lam=par[1]*X[,1]+par[2]*X[,2]+par[3]*X[,3]
#neg log-likelihood
sum(-dpois(y,lambda = exp(lam),log = TRUE))
}Numerical Optim. for MLEs
Comparison
(Intercept) siteSite 2 siteSite 3
glm.fit 0.6549253 -1.011598 0.1221050
ours 0.6549260 -1.011601 0.1221027Control over Dummy Coding
Make ‘Site 2’ the intercept
Call:
glm(formula = y ~ site.re, family = poisson(link = "log"), data = dat)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.3567 0.1890 -1.887 0.0591 .
site.reSite 1 1.0116 0.2207 4.584 4.56e-06 ***
site.reSite 3 1.1337 0.2173 5.218 1.81e-07 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 341.36 on 119 degrees of freedom
Residual deviance: 305.76 on 117 degrees of freedom
AIC: 496.33
Number of Fisher Scoring iterations: 6Same Model Different Estimates
Coeficients
(Intercept) siteSite 2 siteSite 3
Model1 0.6549 -1.0116 0.1221
Model2 -0.3567 1.0116 1.1337Predictions
1 2 3 4 5
Model1 1.925 0.7 2.175 1.925 0.7
Model2 1.925 0.7 2.175 1.925 0.7Design Matrix
(Intercept) dat$siteSite 2 dat$siteSite 3
1 1 0 0
2 1 1 0
3 1 0 1
4 1 0 0
5 1 1 0 (Intercept) dat$site.reSite 1 dat$site.reSite 3
1 1 1 0
2 1 0 0
3 1 0 1
4 1 1 0
5 1 0 0More Control!
Deviation Coding Interpretation
Intercept = grand mean of site-means (log-scale), not mean of all observations
\(\beta_{0} + \beta_{1} \times 1 + \beta_{2}\times 0\)
\(0.3584266 + 0.2964994 \times 1 + 0\)
\(\beta_{1}\) = effect difference of Site 1 from Grand Mean
\(\beta_{2}\) = effect difference of Site 2 from Grand Mean
Intuition Check
site x
1 Site 1 1.925
2 Site 2 0.700
3 Site 3 2.175More Control Again
Contrasts
No shared connection among these partial intercepts
Same Model Different Estimates
Coeficients
(Intercept) siteSite 2 siteSite 3
Model1 0.6549260 -1.0116009 0.1221027
Model2 -0.3566749 1.0116009 1.1337036
Model3 0.3584266 0.2964994 -0.7151015
Model4 0.6549260 -0.3566749 0.7770287Predictions
1 2 3 4 5
Model1 1.925 0.7 2.175 1.925 0.7
Model2 1.925 0.7 2.175 1.925 0.7
Model3 1.925 0.7 2.175 1.925 0.7
Model4 1.925 0.7 2.175 1.925 0.7Deviance
[,1]
Model1 305.7557
Model2 305.7557
Model3 305.7557
Model4 305.7557Taking Control
Poisson Regression (offset)
What if our counts of pika are at plots with different sizes?
Plot size (\(\textbf{A}\)) needs to be controlled for. But, we don’t want to estimate an effect as it’s part of the design. Rather, we want to model the rate - counts per unit area.
\[ \begin{align*} \textbf{y} \sim & \text{Poisson}(\frac{\boldsymbol{\lambda}}{\textbf{A}})\\ \text{log}(\frac{\boldsymbol{\lambda}}{\textbf{A}}) =& \textbf{X}\boldsymbol{\beta} \end{align*} \]
Offset
Equivalent
\[ \begin{align*} \text{log}(\frac{\boldsymbol{\lambda}}{\textbf{A}}) =& \beta_0 + \beta_1 \textbf{x}_{1}\\ \text{log}(\boldsymbol{\lambda}) =& \beta_0 + \beta_1 \textbf{x}_{1} + 1\times \textbf{A} \end{align*} \]
Offset Code
model.rate1 = glm(y~site+offset(log(area)),
data=dat,
family = poisson(link = 'log')
)
model.rate2 = glm(y~site,
offset = log(area),
data=dat,
family = poisson(link = 'log')
)
coef(model.rate1)(Intercept) siteSite 2 siteSite 3
-0.8036891 -0.4692766 -0.0582790 (Intercept) siteSite 2 siteSite 3
-0.8036891 -0.4692766 -0.0582790 Variable Combinations
Additive & Interaction combinations of categorical and continuous variables
- site (categorical)
- herb.cover (continuous)
- dist.trail (continuous)
y site herb.cover dist.trail site.re area
1 0 Site 1 -0.22630093 0.06679655 Site 1 2
2 1 Site 2 0.02221148 -0.24641488 Site 2 5
3 0 Site 3 -1.01517375 -0.73612867 Site 3 2
4 1 Site 1 1.18038309 0.07586011 Site 1 3
5 0 Site 2 -2.04470642 -0.81595409 Site 2 2
6 2 Site 3 2.44433686 0.17929858 Site 3 2Additive
Continuous and Categorical
Linear Combination on log-scale
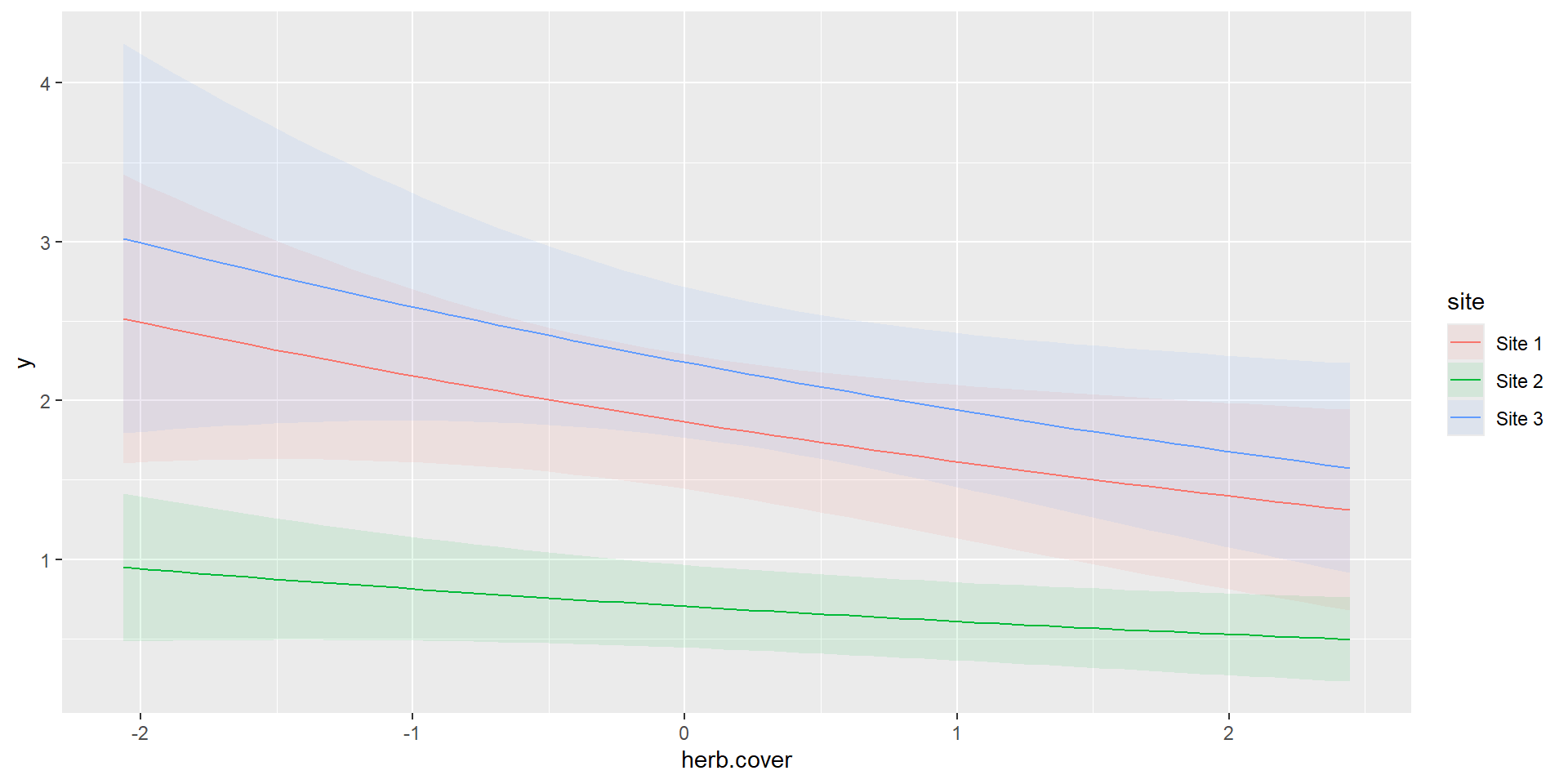
m1 = glm(y~site+herb.cover,data=dat,family = poisson(link = 'log'))
marginaleffects::plot_predictions(m1, condition=c("herb.cover","site"),type="link")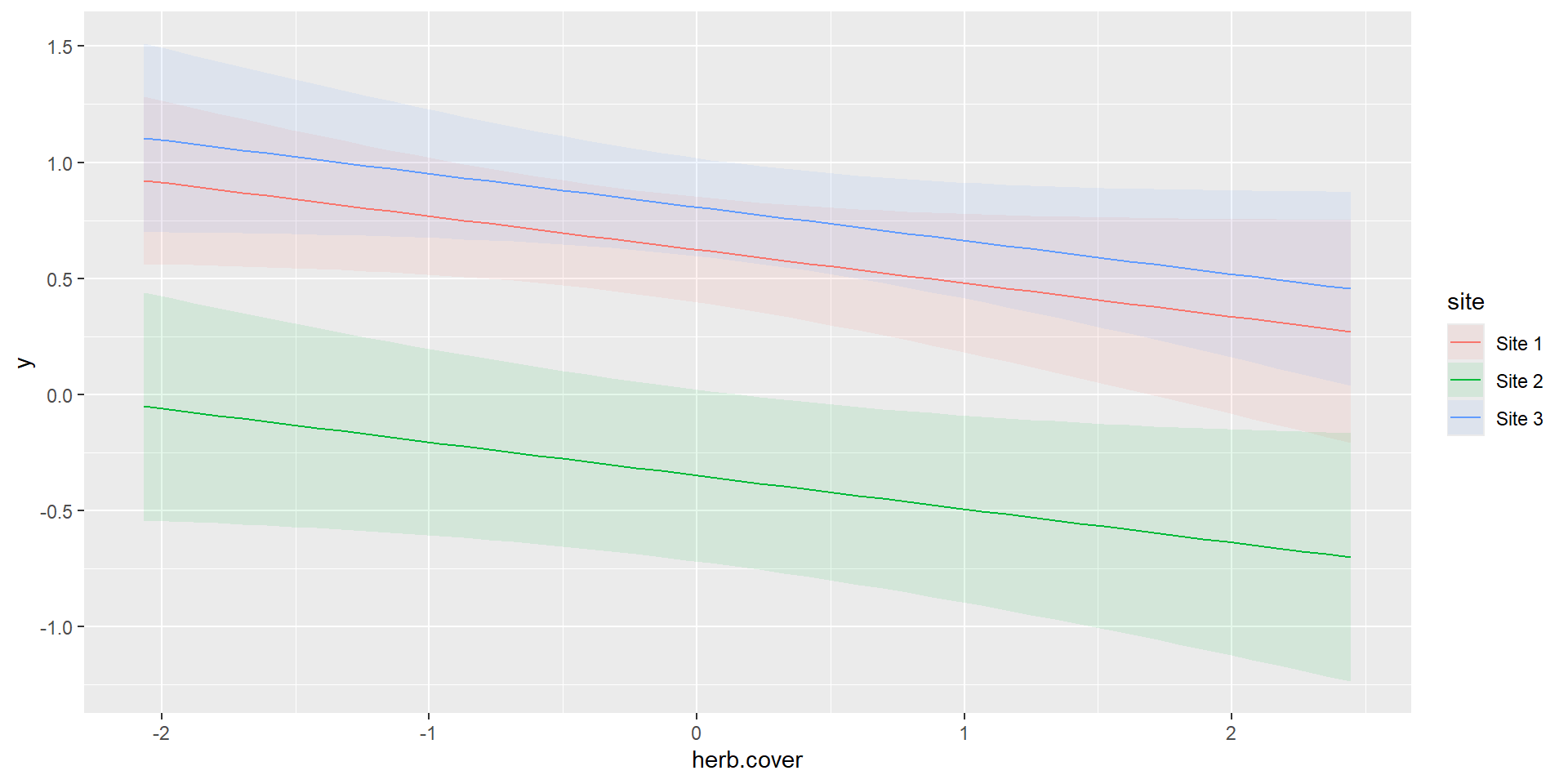
Linear Combination on response-scale
Additive
Continuous and Continuous
Linear Combination on log-scale
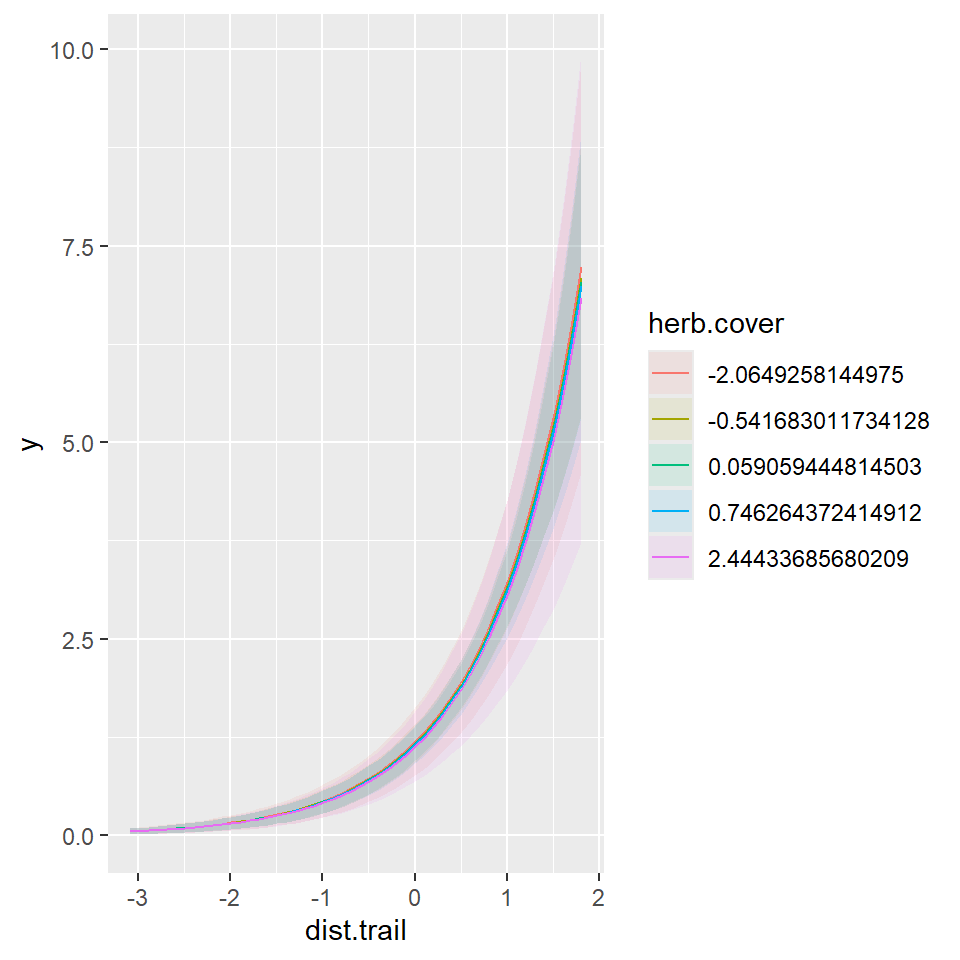
m2 = glm(y~dist.trail+herb.cover,data=dat,family = poisson(link = 'log'))
marginaleffects::plot_predictions(m2,
condition=c("dist.trail","herb.cover"),
type="link")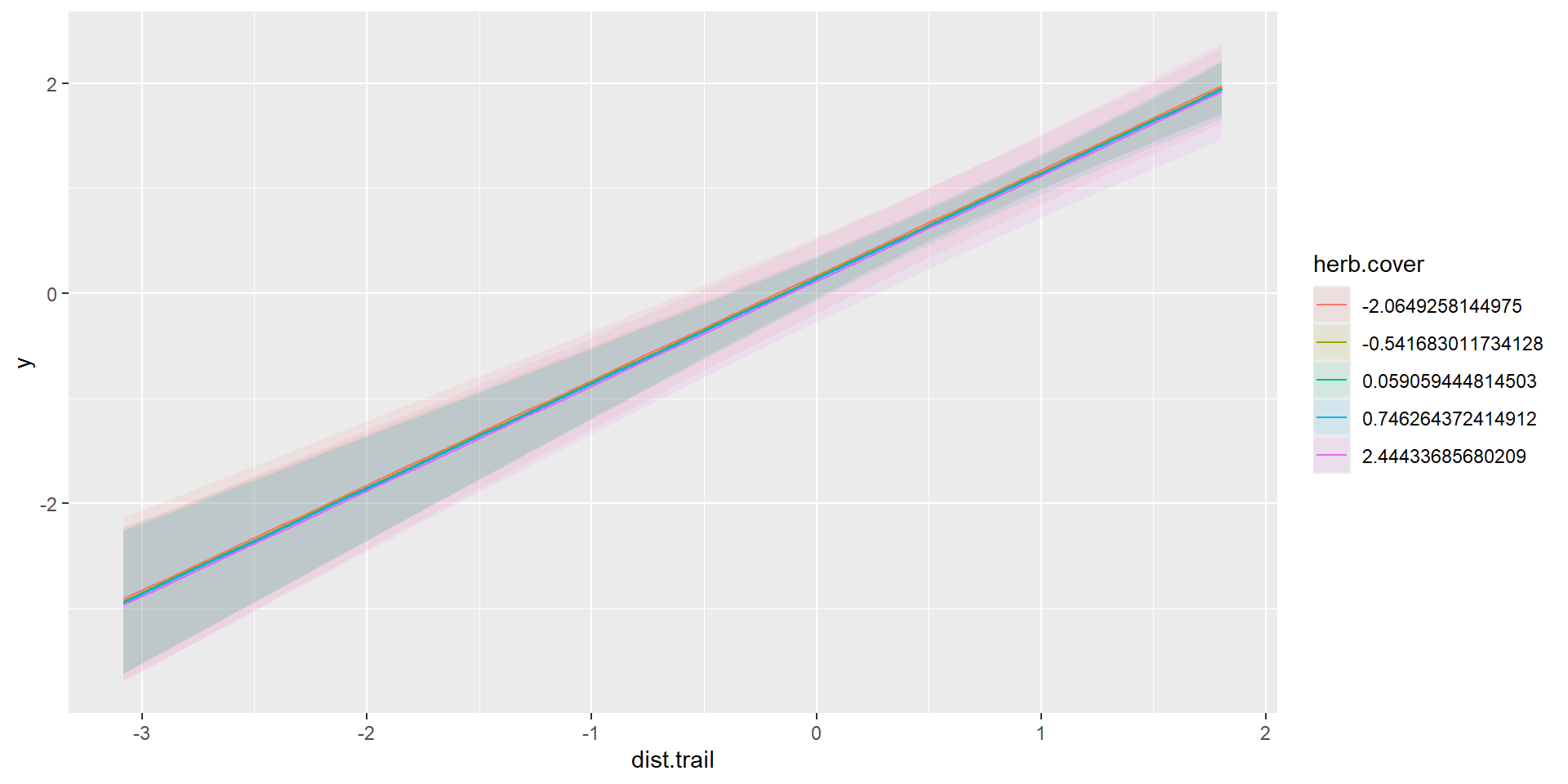
Linear Combination on response-scale
Interaction
Continuous and Categorical
m3 = glm(y~site*herb.cover,data=dat,family = poisson(link = 'log'))
m3 = glm(y~site+herb.cover+site:herb.cover,data=dat,family = poisson(link = 'log'))
head(model.matrix(~site*herb.cover,data=dat)) (Intercept) siteSite 2 siteSite 3 herb.cover siteSite 2:herb.cover
1 1 0 0 -0.22630093 0.00000000
2 1 1 0 0.02221148 0.02221148
3 1 0 1 -1.01517375 0.00000000
4 1 0 0 1.18038309 0.00000000
5 1 1 0 -2.04470642 -2.04470642
6 1 0 1 2.44433686 0.00000000
siteSite 3:herb.cover
1 0.000000
2 0.000000
3 -1.015174
4 0.000000
5 0.000000
6 2.444337Interaction
Continuous and Categorical
Call:
glm(formula = y ~ site + herb.cover + site:herb.cover, family = poisson(link = "log"),
data = dat)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.2495 0.1609 1.551 0.1209
siteSite 2 -0.6522 0.2561 -2.546 0.0109 *
siteSite 3 0.4728 0.1987 2.379 0.0174 *
herb.cover -0.9102 0.1626 -5.597 2.18e-08 ***
siteSite 2:herb.cover 1.1299 0.2665 4.240 2.24e-05 ***
siteSite 3:herb.cover 1.0650 0.1948 5.466 4.61e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 341.36 on 119 degrees of freedom
Residual deviance: 267.16 on 114 degrees of freedom
AIC: 463.74
Number of Fisher Scoring iterations: 6Interaction
Continuous and Categorical
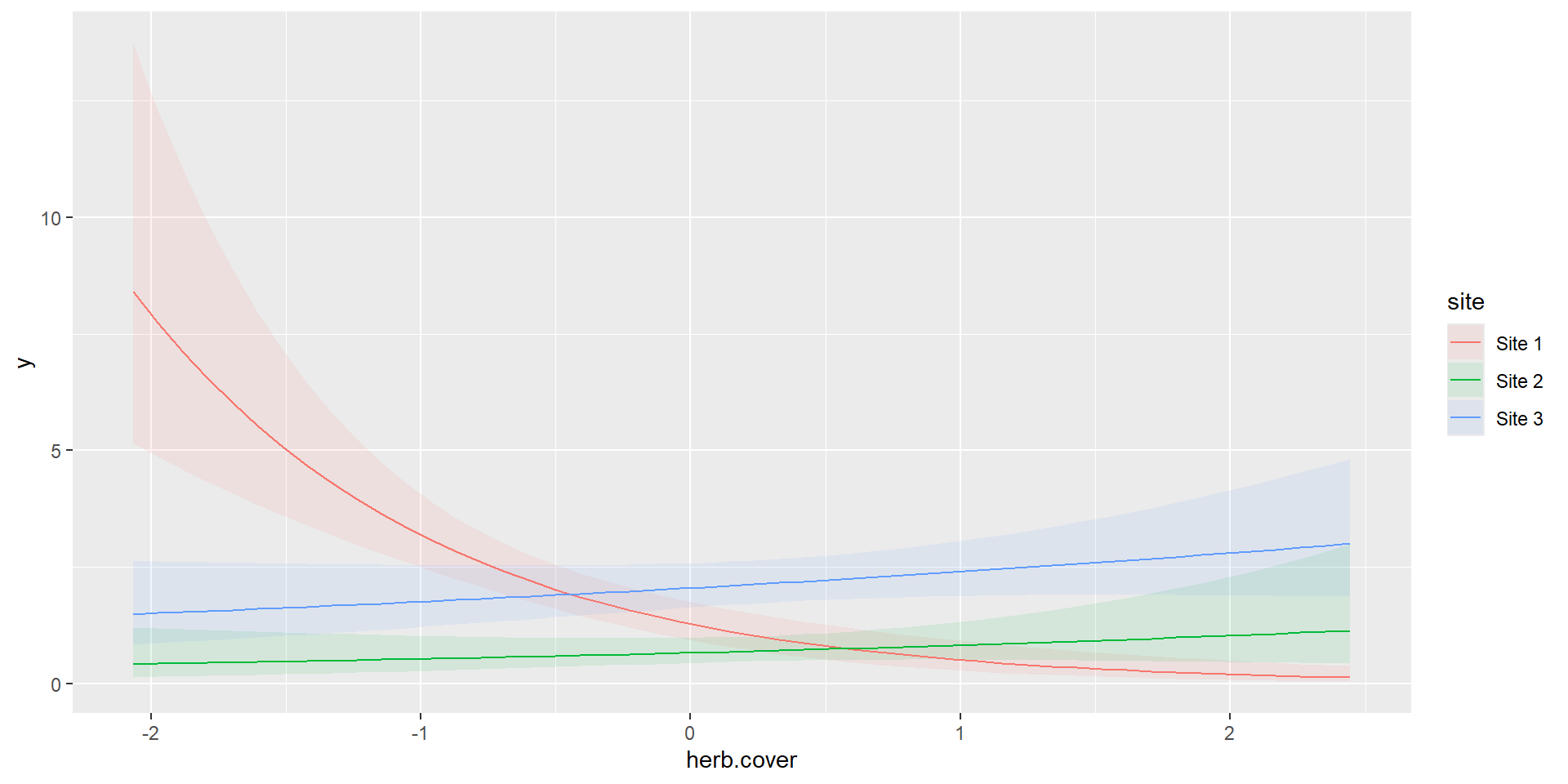
Interaction
Continuous and Continuous
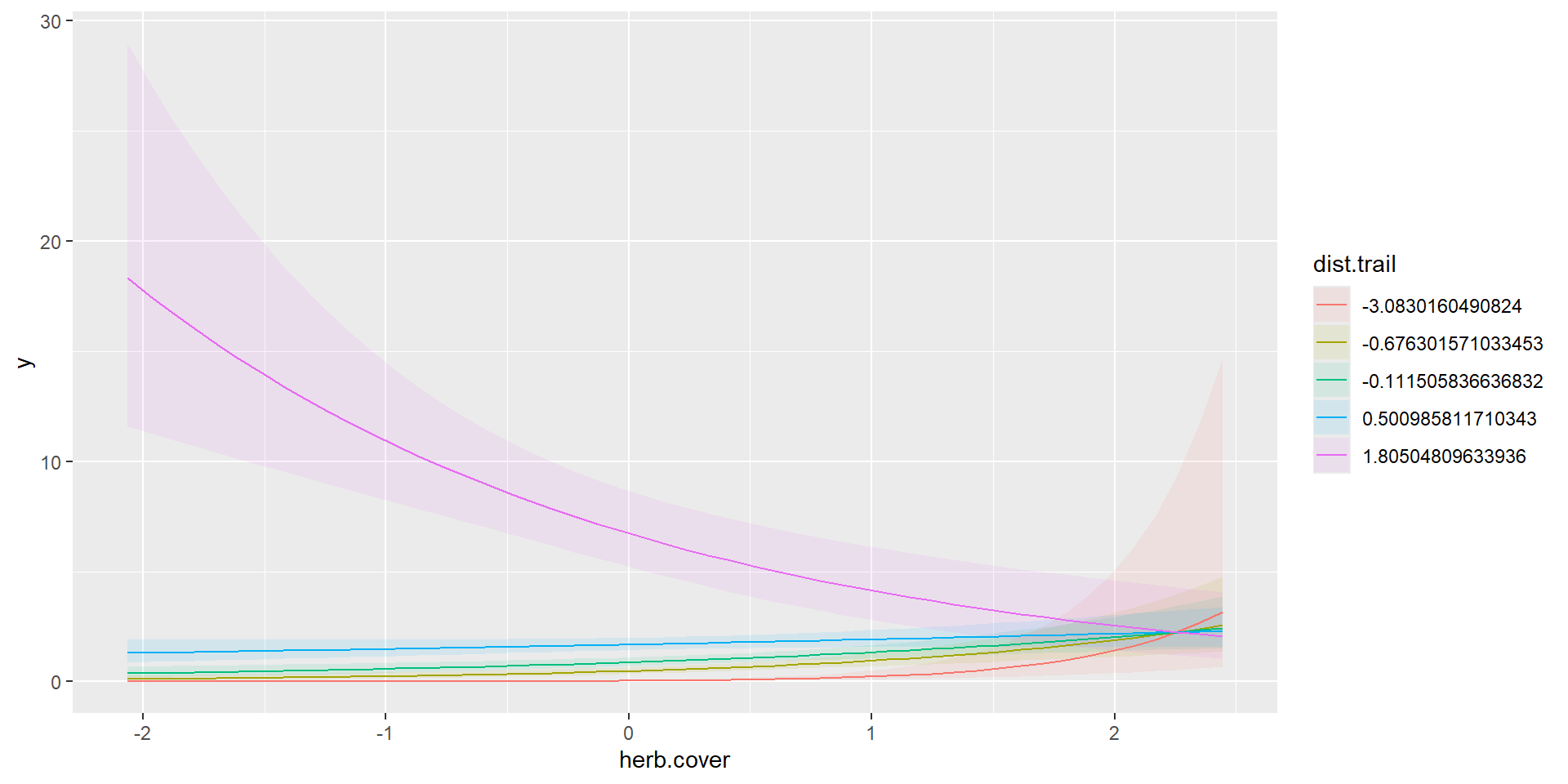
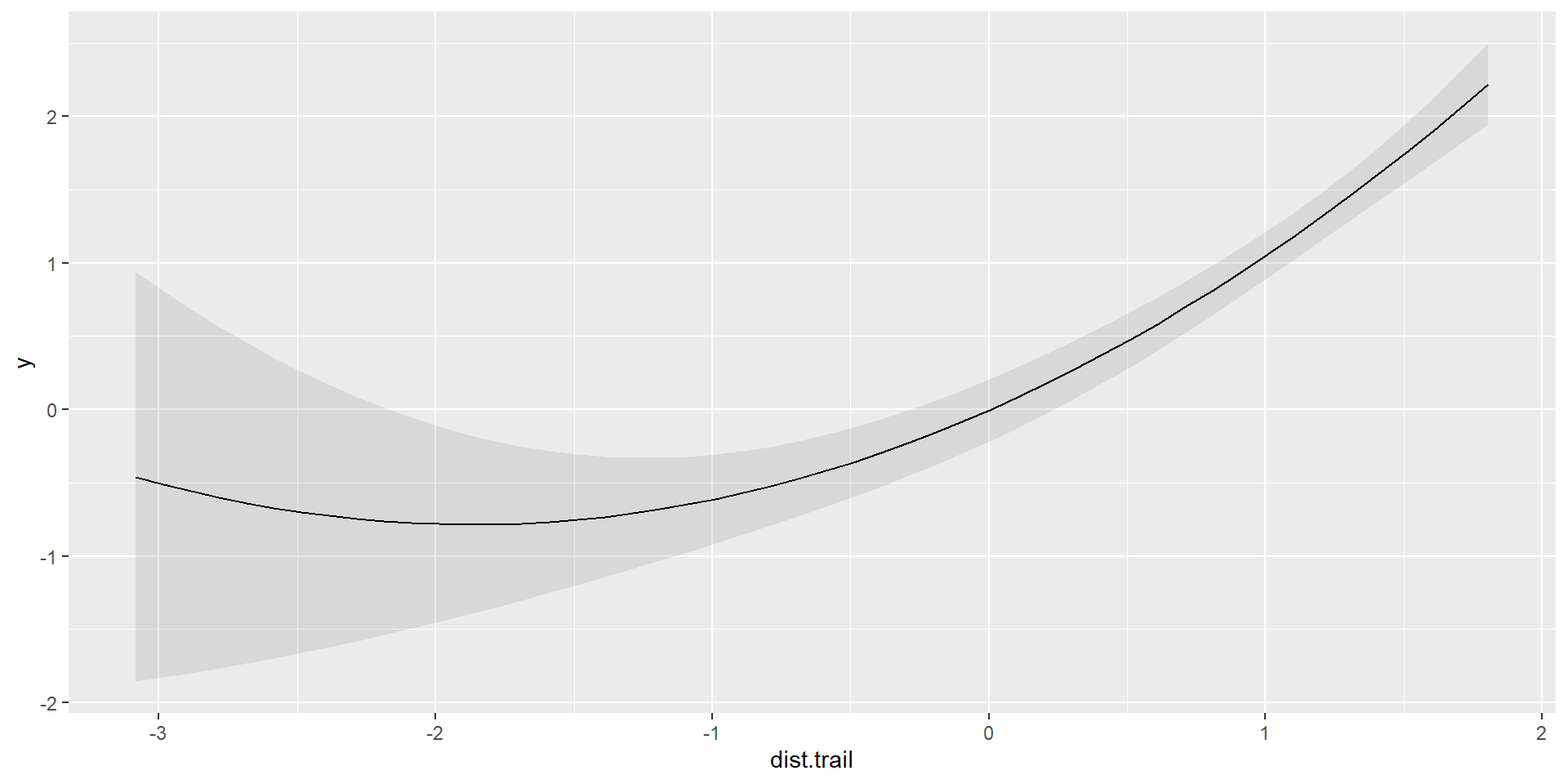
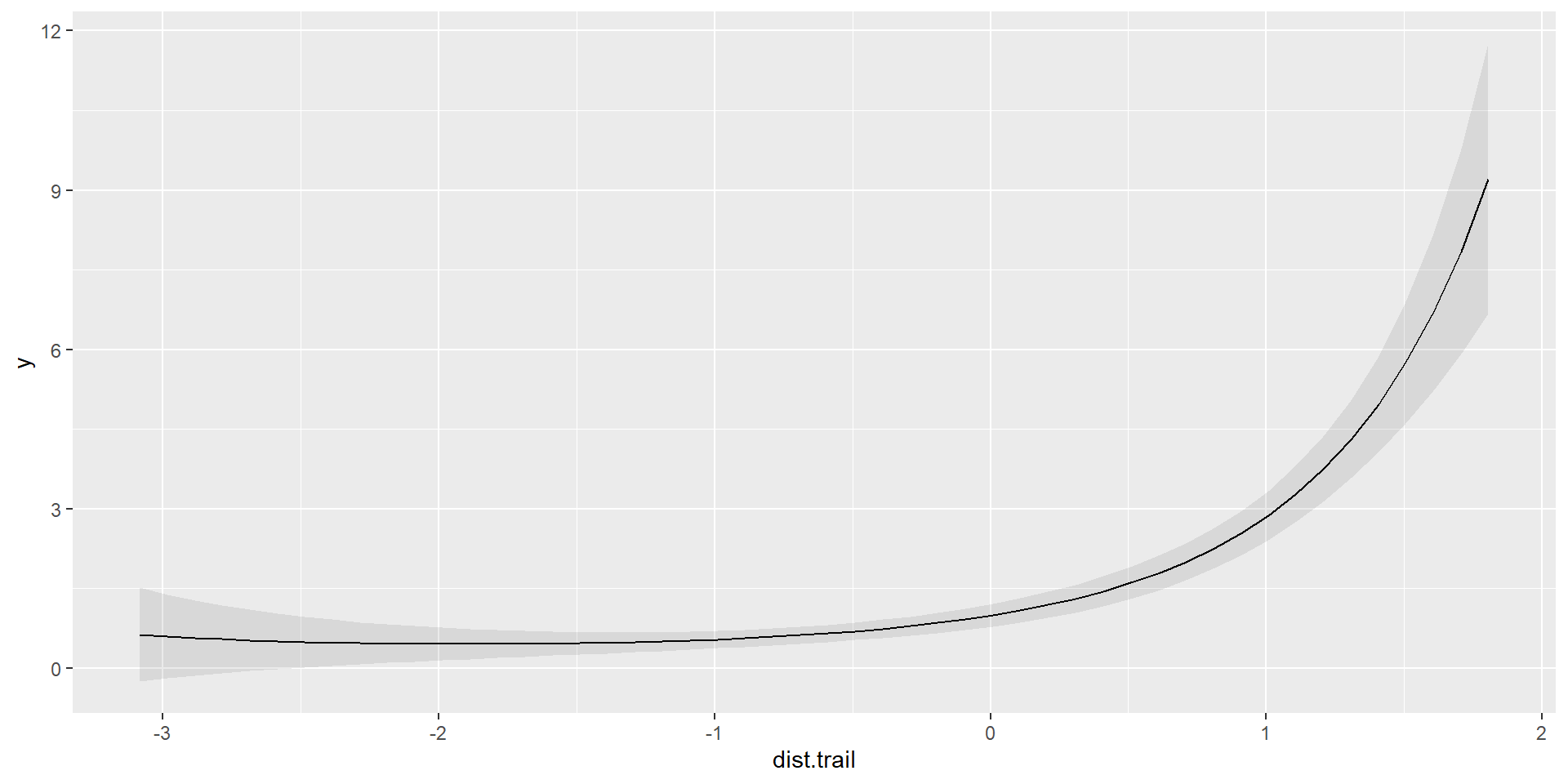
Polynomial
Quadratic
Recap
- Poisson Regression
- Numerical Optimization
- Categorical variables >2 levels
- Effect Coding
- Variable Combinations