par(mfrow=c(1,2))
hist(y, breaks=20,xlim=c(0,25),main=main)
hist(y, breaks=20,xlim=c(0,25),freq = FALSE,main=main)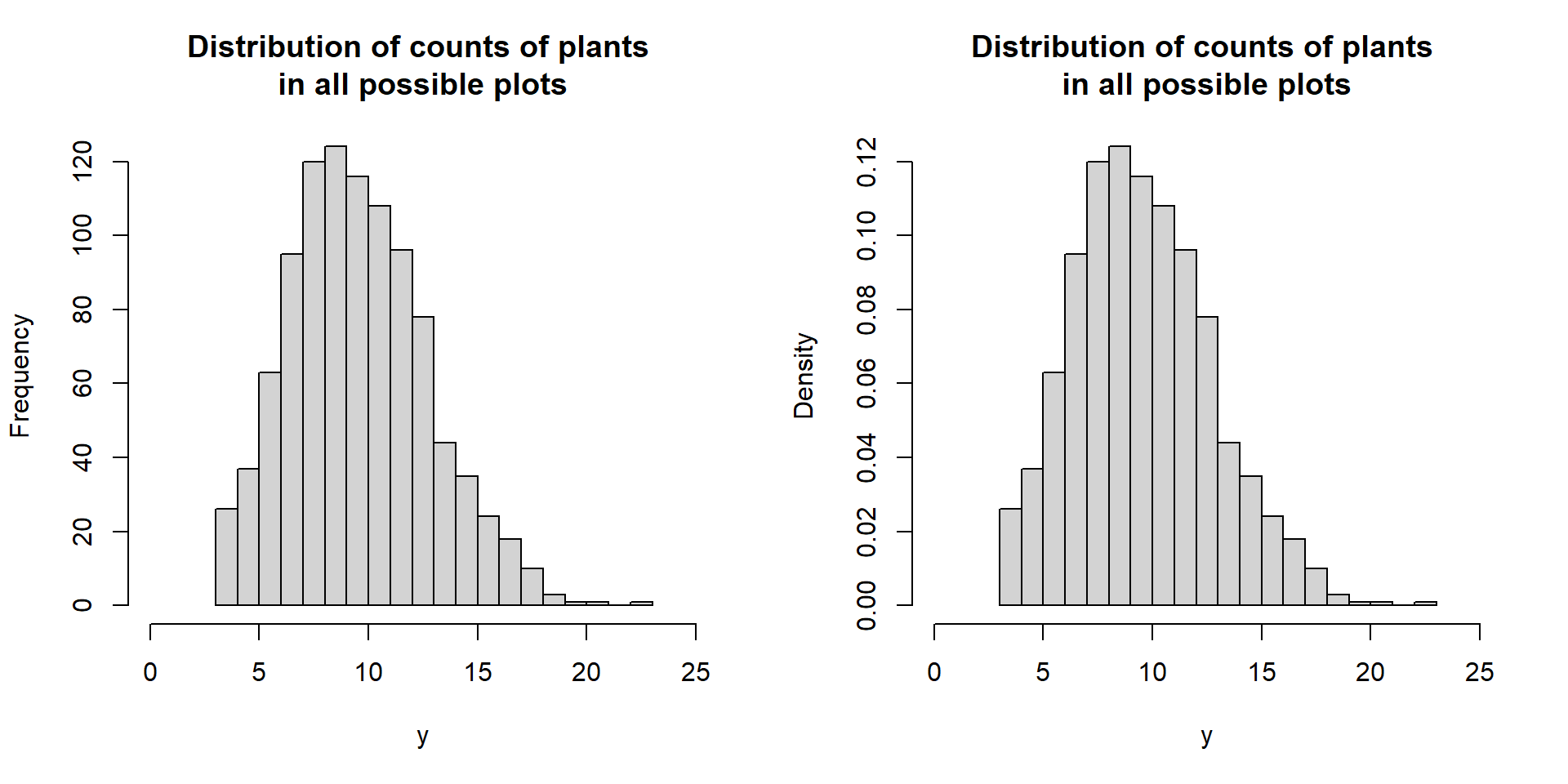
Connect random variables, probabilities, and parameters
define prob. functions
use/plot prob. functions
learn some notation
Probability and statistics are the opposite sides of the same coin.
To understand statistics, we need to understand probability and probability functions.
The two key things to understand this connection is the random variable (RV) and parameters (e.g., \(\theta\), \(\sigma\), \(\epsilon\), \(\mu\)).
Why learn about RVs and probability math?
Foundations of:
Our Goal:
\[ \begin{align*} a =& 10 \\ b =& \text{log}(a) \times 12 \\ c =& \frac{a}{b} \\ y =& \beta_0 + \beta_1*c \end{align*} \]
All variables here are scalars. They are what they are and that is it. \(\beta\) variables and \(y\) are currently unknown, but still scalars.
Scalars are quantities that are fully described by a magnitude (or numerical value) alone.
\[ y \sim f(y) \]
\(y\) is a random variable which may change values each observation; it changes based on a probability function, \(f(y)\).
The tilde (\(\sim\)) denotes “has the probability distribution of”.
Which value (y) is observed is predictable. Need to know parameters (\(\theta\)) of the probability function \(f(y)\).
Specifically, \(f(y|\theta)\), where ‘|’ is read as ‘given’.
Toss of a coin
Roll of a die
Weight of a captured elk
Count of plants in a sampled plot
The values observed can be understand based on the frequency within the population or presumed super-population. These frequencies can be described by probabilities.
par(mfrow=c(1,2))
hist(y, breaks=20,xlim=c(0,25),main=main)
hist(y, breaks=20,xlim=c(0,25),freq = FALSE,main=main)
We often only get to see ONE sample from this distribution.

We are often interested in the characteristics of the whole population of frequencies,
We infer what these are based on our sample (i.e., statistical inference).
Frequentist Paradigm:
Data (e.g., \(y\)) are random variables that can be described by probability distributions with unknown parameters that (e.g., \(\theta\)) are fixed (scalars).
Bayesian Paradigm:
Data (e.g., \(y\)) are random variables that can be described by probability functions where the unknown parameters (e.g., \(\theta\)) are also random variables that have probability functions that describe them.
\[ \begin{align*} y =& \text{ event/outcome} \\ f(y|\boldsymbol{\theta}) =& [y|\boldsymbol{\theta}]= \text{ process governing the value of } y \\ \boldsymbol{\theta} =& \text{ parameters} \\ \end{align*} \]
\(f()\) or [ ] is conveying a function (math).
It is called a PDF when \(y\) is continuous and a PMF when \(y\) is discrete.
We commonly use deterministic functions (indicated by non-italic letter); e.g., log(), exp(). Output is always the same with the same input. \[ \hspace{-12pt}\text{g} \\ x \Longrightarrow\fbox{DO STUFF } \Longrightarrow \text{g}(x) \]
\[ \hspace{-14pt}\text{g} \\ x \Longrightarrow\fbox{+7 } \Longrightarrow \text{g}(x) \]
\[ \text{g}(x) = x + 7 \]
Probability: Interested in \(y\), the data, and the probability function that “generates” the data. \[ \begin{align*} y \leftarrow& f(y|\boldsymbol{\theta}) \\ \end{align*} \]
Statistics: Interested in population characteristics of \(y\); i.e., the parameters,
\[ \begin{align*} y \rightarrow& f(y|\boldsymbol{\theta}) \\ \end{align*} \]
Special functions with rules to guarantee our logic of probabilities are maintained.
\(y\) can only be a certain set of values.
These sets are called the sample space (\(\Omega\)) or the support of the RV.
\[ f(y) = P(Y=y) \]
Data has two outcomes (0 = dead, 1 = alive)
\(y \in \{0,1\}\)
There are two probabilities
Axiom 1: The probability of an event is greater than or equal to zero and less than or equal to 1.
\[ 0 \leq f(y) \leq 1 \] Example,
Axiom 2: The sum of the probabilities of all possible values (sample space) is one.
\[ \sum_{i} f(y_i) = f(y_1) + f(y_2) + ... = P(\Omega) =1 \] Example,
Still need to define \(f()\), our PMF for \(y \in \{0,1\}\)
\[ f(y|\theta) = [y|\theta]= \begin{align} \theta^{y}\times(1-\theta)^{1-y} \end{align} \]
\(\theta\) = P(Y = 1) = 0.2
\[ f(y|\theta) = [y|\theta]= \begin{align} = 0.2^{1}\times(1-0.2)^{0-0} \end{align} \]
\[ f(y|\theta) = [y|\theta]= \begin{align} = 0.2 \times (0.8)^{0} = 0.2 \end{align} \]
\[ f(y|\theta) = [y|\theta]= \begin{align} \theta^{y}\times(1-\theta)^{1-y} \end{align} \]
Sample space support (\(\Omega\)):
Parameter space support (\(\Theta\)):
What would our data look like for 10 ducks that had a probability of survival (Y=1) of 0.20?
How about to evaluate the sample size of ducks needed to estimate \(\theta\)?
The Bernoulli is a special case of the Binomial Distribution.
\[ f(y|\theta) = [y|\theta]= \begin{align} {N\choose y} \theta^{y}\times(1-\theta)^{N-y} \end{align} \]
\(N\) = total trials / tagged and released animals
\(y\) = number of successes / number of alive animals at the of the study.
[1] 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 1 0
[38] 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0
[75] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
[112] 1 1 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 0 1 0 0
[149] 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0
[186] 1 0 0 1 0 1 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0
[223] 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 0 0 1 0 0
[260] 0 1 1 0 0 1 0 0 0 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0
[297] 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0
[334] 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0
[371] 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 1
[408] 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0
[445] 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0
[482] 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
[519] 0 0 1 1 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 1 0 0 1 0 1 0 0 1 1 0 0 0 1 0 1 0 0
[556] 1 0 0 0 1 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 0
[593] 1 0 0 0 0 0 0 1 1 0 1 0 0 1 1 0 0 0 0 0 0 1 0 0 1 0 0 0 1 0 0 1 0 0 0 0 0
[630] 0 1 0 1 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 1 0 1
[667] 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0
[704] 0 1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0
[741] 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1
[778] 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1
[815] 0 1 0 0 0 1 1 0 1 0 0 0 0 0 0 1 1 0 1 0 0 1 0 0 1 0 0 0 0 1 1 0 0 0 0 0 0
[852] 1 0 0 0 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0
[889] 0 0 1 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 1 0 1 1 0 0 0 1 1 0 0 0 0
[926] 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 1 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0
[963] 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0
[1000] 0Use a probability function that makes sense for your data/RV. In Bayesian infernece, we also pick prob. functions that make sense for parameters.
The sample space and parameter support can be found on Wikipedia for many probability functions.
For example, the Normal/Gaussian distribution describes the sample space for all values on the real number line.
\[y \sim \text{Normal}(\mu, \sigma) \\ y \in (-\infty, \infty) \\ y \in \mathbb{R}\]
What is the parameter space for \(\mu\) and \(\sigma\)?
We collect data on adult alligator lengths (in).
[1] 90.30 83.02 103.67 85.17 99.20 106.74 90.76 105.28 99.41 101.72
Should we use the Normal Distribution
to estimate the mean?
Does the support of our data match
the support of the PDF?
What PDF does?
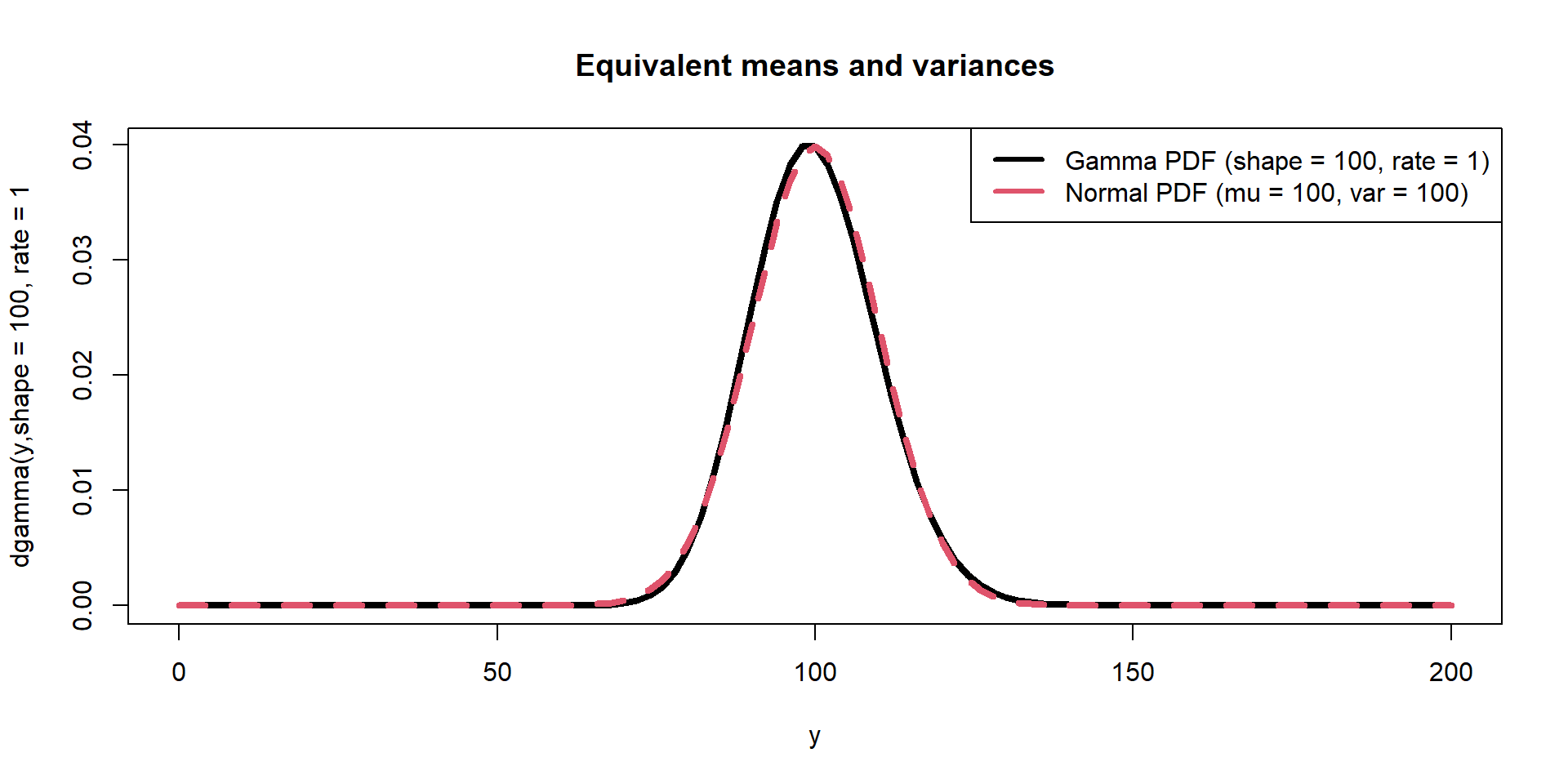
Are they exactly the same?
The issue is when the data are near 0, we might estimate non-sensical values (e.g. negative).
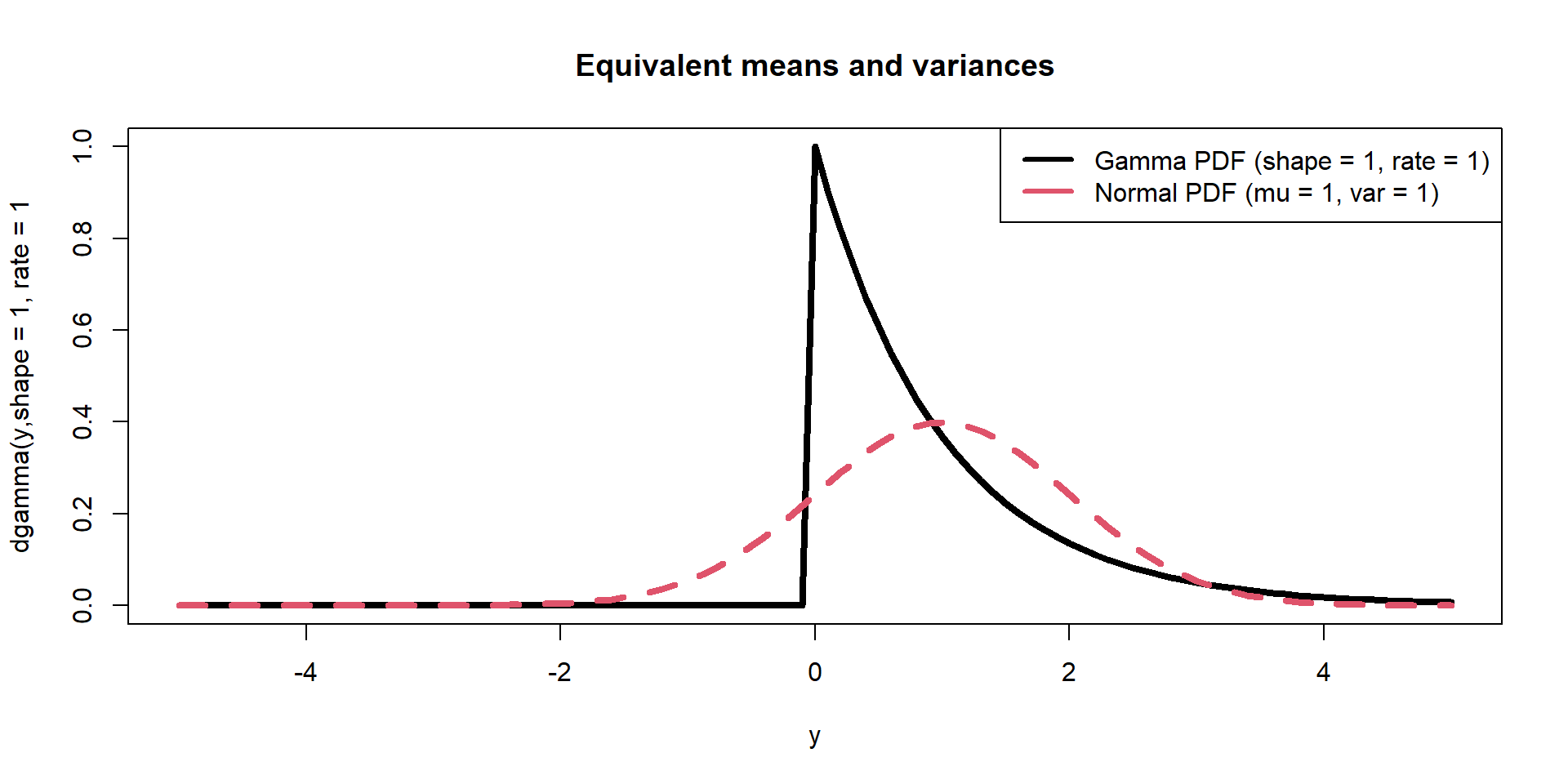
\(y\) are an uncountable set of values.
Provide ecological data examples that match the support?
PDFs of continious RVs follow the same rules as PMFs.
Axiom 1:
PDFs output probability densities, not probabilities.
Axiom 2:
\[ y \sim \text{Normal}(\mu, \sigma) \\ f(y|\mu,\sigma ) = \frac{1}{\sigma\sqrt{2\pi}}e^{\frac{1}{2}(\frac{y-\mu}{\sigma})^{2}} \\ \]
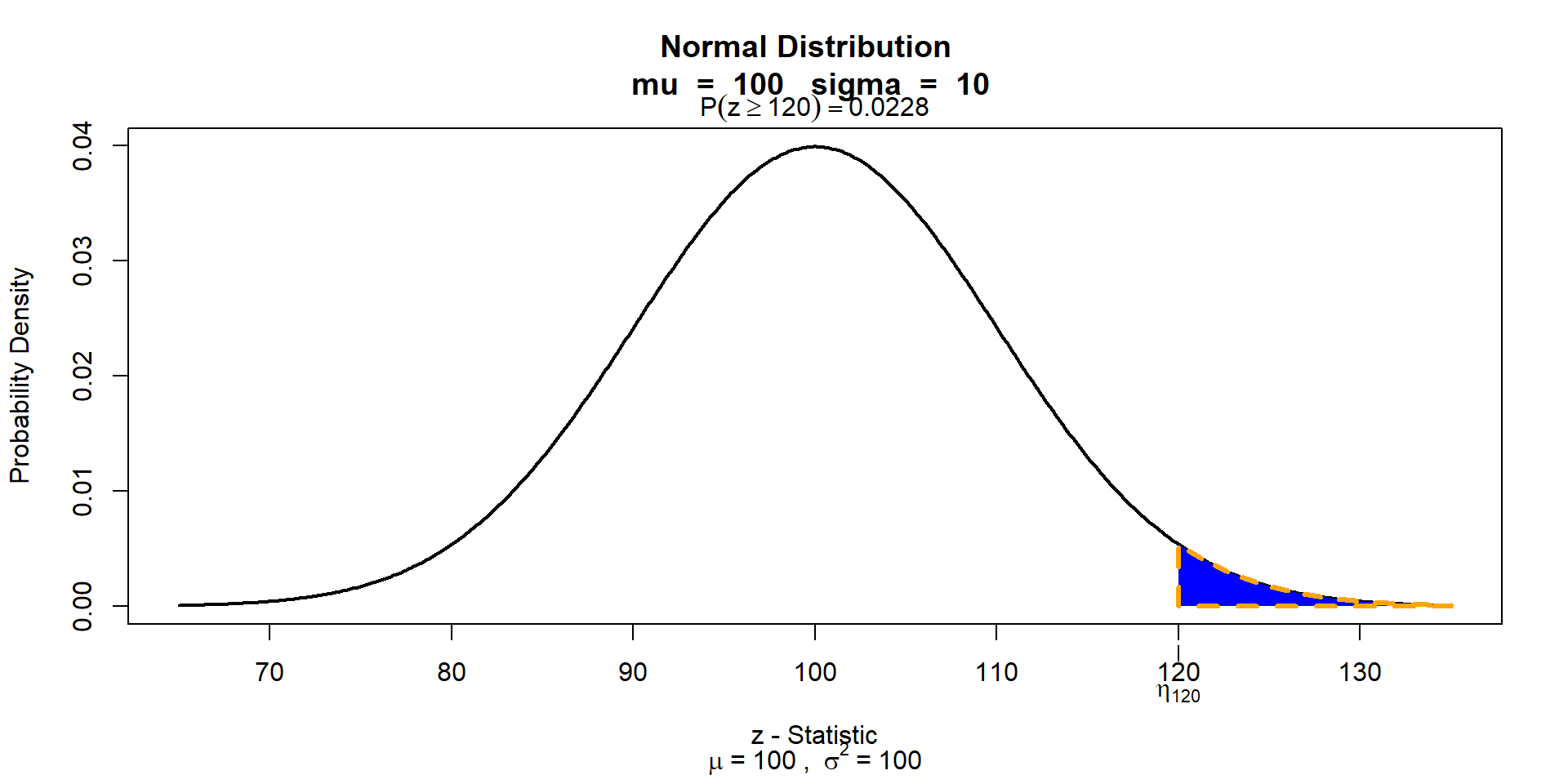
The math,
\[ \int_{120}^{\infty} f(y| \mu, \sigma)dy = P(120<Y<\infty) \]
Read this as “the integral of the probability density function between 120 and infinity (on the left-hand side) is equal to the probability that the outcome of the random variable is between 120 and infinity (on the right-hand side)”.
Axiom 3:
The sum of the probability densities of all possible outcomes is equal to 1.
Properties of all probability functions.
Normal Distribution: parameters (\(\mu\) and \(\sigma\)) are 1\({^{st}}\) and 2\({^{nd}}\) moments
Gamma Distribution: parameters are not moments
Shape = \(\alpha\), Rate = \(\beta\)
OR
Shape = \(\kappa\), Scale = \(\theta\), where \(\theta = \frac{1}{\beta}\)
NOTE: probability functions can have Alternative Parameterizations, such they have different parameters.
Moments are functions of these parameters:
mean = \(\kappa\theta\) or \(\frac{\alpha}{\beta}\)
var = \(\kappa\theta^2\) or \(\frac{\alpha}{\beta^2}\)
Probability: Interested in the variation of y, \[ \begin{align*} y \leftarrow& f(y|\boldsymbol{\theta'}) \\ \end{align*} \]
\[ \begin{align*} \boldsymbol{\theta'} =& \begin{matrix} [\kappa & \theta] \end{matrix} \\ f(y|\boldsymbol{\theta}') &= \text{Gamma(}\kappa, \theta) \\ \end{align*} \]
\[ \begin{align*} f(y|\boldsymbol{\theta}') &= \frac{1}{\Gamma(\kappa)\theta^{\kappa}}y^{\kappa-1} e^{-y/\theta} \\ \end{align*} \]
What is the probability we would sample a value >40?
In this population, how common is a value >40?
\[ \begin{align*} p(y>40) = \int_{40}^{\infty} f(y|\boldsymbol{\theta}) \,dy \end{align*} \]
What is the probability of observing \(y\) < 20
What is the probability of observing 20 < \(y\) < 40
[1] 0.4529343Reverse the question: What values of \(y\) and lower have a probability of 0.025
What values of \(y\) and higher have a probability of 0.025
Statistics: Interested in estimating population-level characteristics; i.e., the parameters
\[ \begin{align*} y \rightarrow& f(y|\boldsymbol{\theta}) \\ \end{align*} \]
REMEMBER
\(f(y|\boldsymbol{\theta})\) is a probability statement about \(y\), NOT \(\boldsymbol{\theta}\).