Random Response
Surveys
What do we use surveys for in our field?
 ## Non-Sampling Error
## Non-Sampling Error
- Differences b/w estimate and true population quantities that do not arise because you didn’t observe the whole population

Non-Sampling Error
Examples??
- Sensitive topics
- detection errors
Dealing with non-response
- Prevent it through the design (best solution!)
- Ignore it (common and may lead to bias)
- Take representative subsample of non-respondents
- Use a model / make assumptions
Random Response Survey
How can we deal with non-response and “wrong” responses?

Warner, S. L. (1965). Randomized response: A survey technique for eliminating evasive answer bias. Journal of the American statistical association, 60, 63-69.
Random Response Survey
Combine probability math and a survey technique to ask your question indirectly
- First: you need a mechanism to receive an answer w/o knowing which question is being asked
- Second: you need to know the probability of the question
- Third: record the answers, frequency of yes and no’s
Random Response Survey
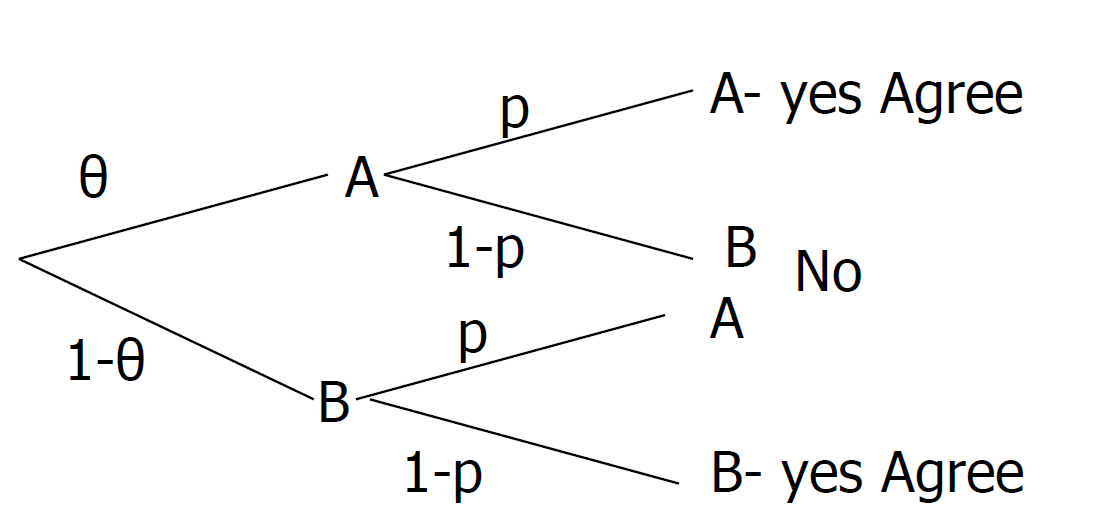
Start with identical note cards with a fraction (\(\theta\); this has to be known) marked with \(A\) and the remaining \((1- \theta)\) marked with \(B\).
If \(A\), answer the question, e.g.,
- have you ever cheated on an exam
If \(B\), answer the question, e.g.,
- have you never cheated on an exam
A sample of people are chosen; each is asked to randomly draw a card and state ‘yes’ if they agree with the letter on the card or ‘no’ otherwise.
The interviewer does not ever see the card – just records ‘yes’ or ‘no’.
Random Response Estimator
Random Response Estimator
\[ \frac{n_{\text{yes}}}{n_{\text{total}}} = \theta p+(1-\theta)\times(1-p) \]
Random Response Estimator
\[
\hat{p} = \frac{1}{2\theta-1} \frac{n_{\text{yes}}}{n_{\text{total}}}-\frac{1-\theta}{2\theta-1}\text{where }\theta\ne0.5
\]
\[ \hat{\sigma}^2_p = \frac{1}{n_{\text{total}}}\left( \frac{1}{16(\theta-0.5)^2}- (p-0.5)^2\right) \]
Lots of variations
- flip a coin to pick the question
- Q1) primary, Q2) whether your phone number ends with an odd number
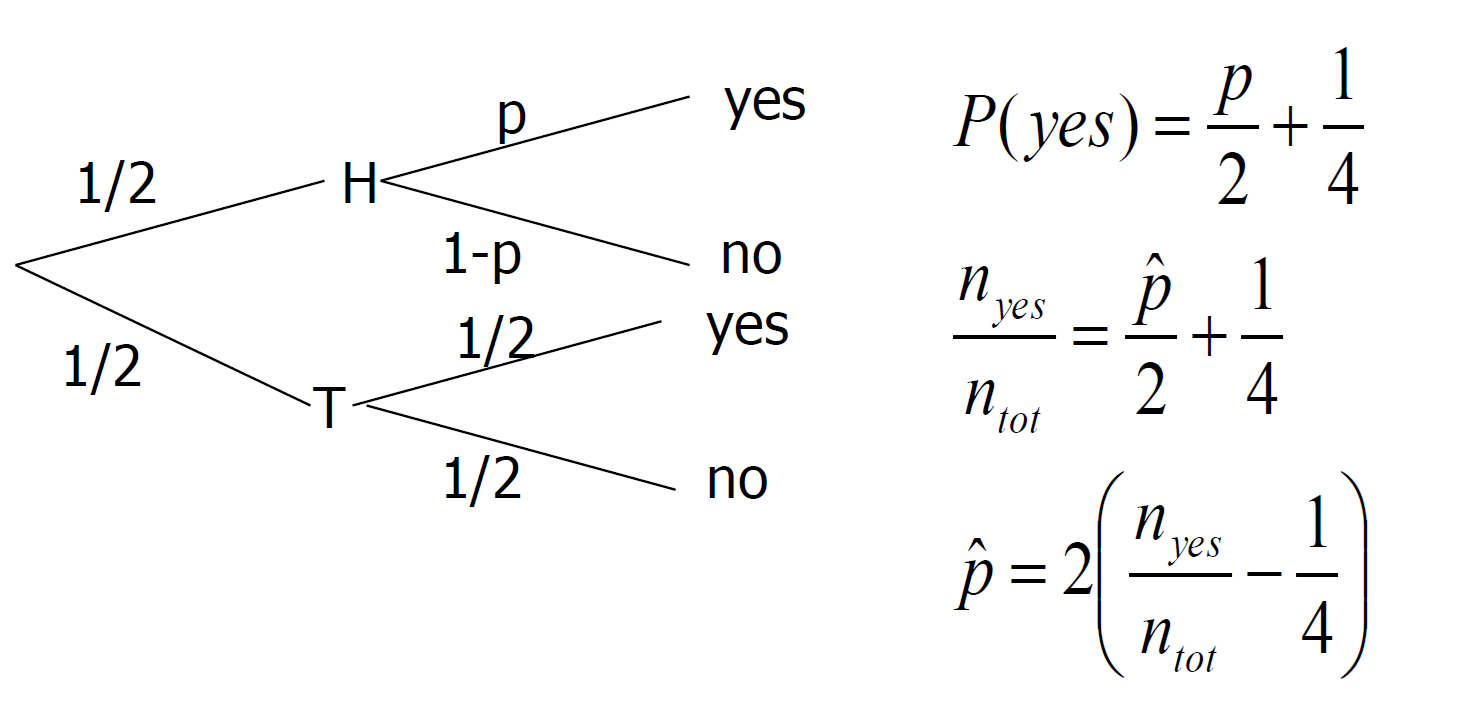
Test it?
What’s our question?
Evaluate the Estimator
Let’s consider how the sample size (\(n\)) effects the sampling distribution of \(\hat{p}\)
Also, consider how our choice of \(\theta\) effect the sampling distribution of \(\hat{p}\)