Sample Size

How many samples?

Most common question

• depends on sampling
• depends on design
• depends on objective

Population Mean

Sample size (n) for estimating the population mean (Thompson Ch. 4, Eqn 3)

\[ n = \frac{1}{d^2/(z^{2}\sigma^2)+(1/N)} \]

• \(d\) = absolute difference b/w population mean and estimate
• \(d\) = \(\lvert{\mu- \hat{\mu}}\lvert\)
• \(N\) = total possible sample units
• \(\sigma^2\) = population variance
• \(z\) = upper \(\alpha/2\) of the std. normal dist. (i.e, Normal(0,1))
• \(z_{1-\alpha/2}\) = \(z_{1-0.01/2} = z_{0.99}\) = 2.5758293

Population Mean

Objective: to know the average count of bass with fish lice

• Common in eutrophic lakes throughout North America
• Assuming no error in detecting lice

Population Mean

• N = number of areas in a lake with bass = 200
• Abs. difference (d) is 10
• 99% confidence, \(\alpha = 0.01\)
• \(\sigma = 20\); variation in count across sample units

  N = 200
  d = 10
  alpha  = 0.01
  z = qnorm(1-alpha/2)
  sigma2 = 20^2

  n = 1/(d^2/(z^2*sigma2)+(1/N))
  n

[1] 23.43042

Population Mean

Thompson Ch.4 : “A bothersome aspect of sample size formulas such as these is that they depend on the population variance”.

. . .

Me - “A bothersome aspect of sample size formulas such as these is that they depend on the difference (\(d\)); we know more about \(n\) than \(d\)”.

Population Mean

• You can afford to sample 10 units
• What is the worst level of difference (\(d\)) for
  • 95% confidence level
  • \(\sigma\) could range from 10 to 100
• Use Sample size equation to solve

. . .

How would you solve this?

. . .

This is a HW question

. . .

Work on problem together OR more about sample sizes?

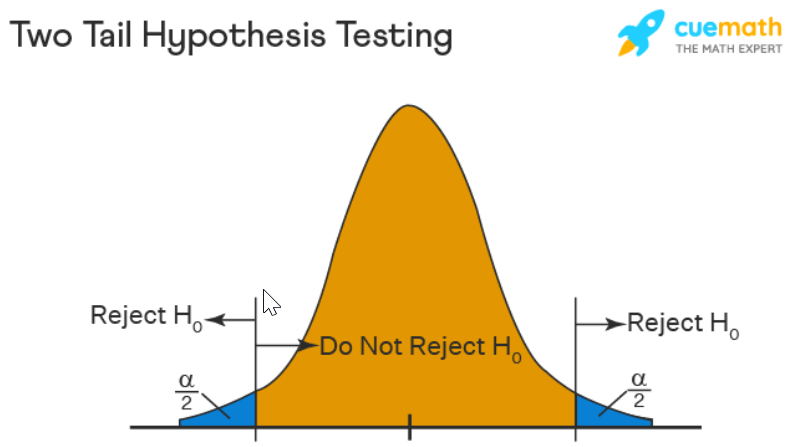
NHT Paradigm

The null hypothesis testing paradigm is often focused on Type I error (\(\alpha\)), rejecting the null hypothesis when it is actually true.

. . .

The Null hypothesis is commonly, \(H_0(\mu_1 = \mu_2)\)

. . .

Statistical Power

• Definition: the probability that a test will reject a false null hypothesis.

  • \(H_0(\mu_1 = \mu_2)\) vs \(H_1(\mu_1 \ne \mu_2)\)

• The higher the statistical power for a given experiment, the lower the probability of making a Type II error (false negative)

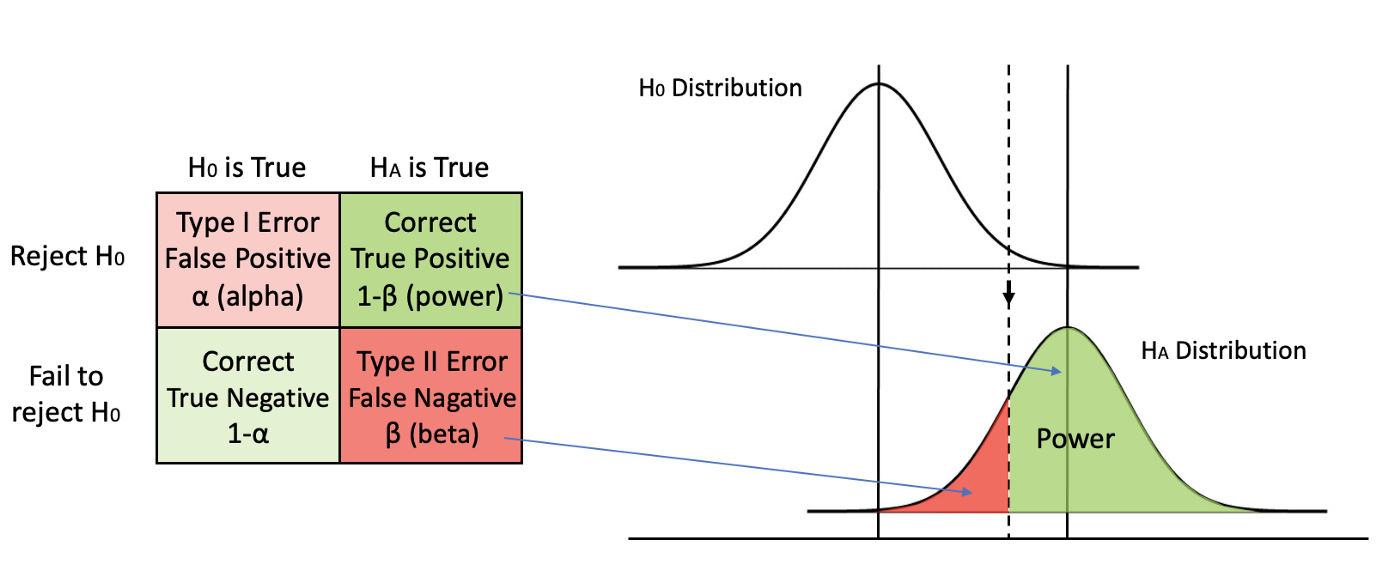
Power Analysis

Type I Error = P(reject \(H_0\) | \(H_0\) is true) = \(\alpha\)

. . .

Power = P(reject \(H_0\) | \(H_1\) is true)

. . .

Power = 1 - Type II Error

. . .

Power = 1 - Pr(False Negative)

. . .

Power = 1 - \(\beta\)

Type II Error / Power

Power Analysis

Contributions to statistical power

• The statistical test and its assumptions

• Effective Sample size (simplest case this is \(n\) per group)

• Reality

  • t-test: difference of means
  • How different these are: \(\mu_{1}\) and \(\mu_{2}\)
  • How variable these are: \(\sigma_{1}\) and \(\sigma_{2}\)

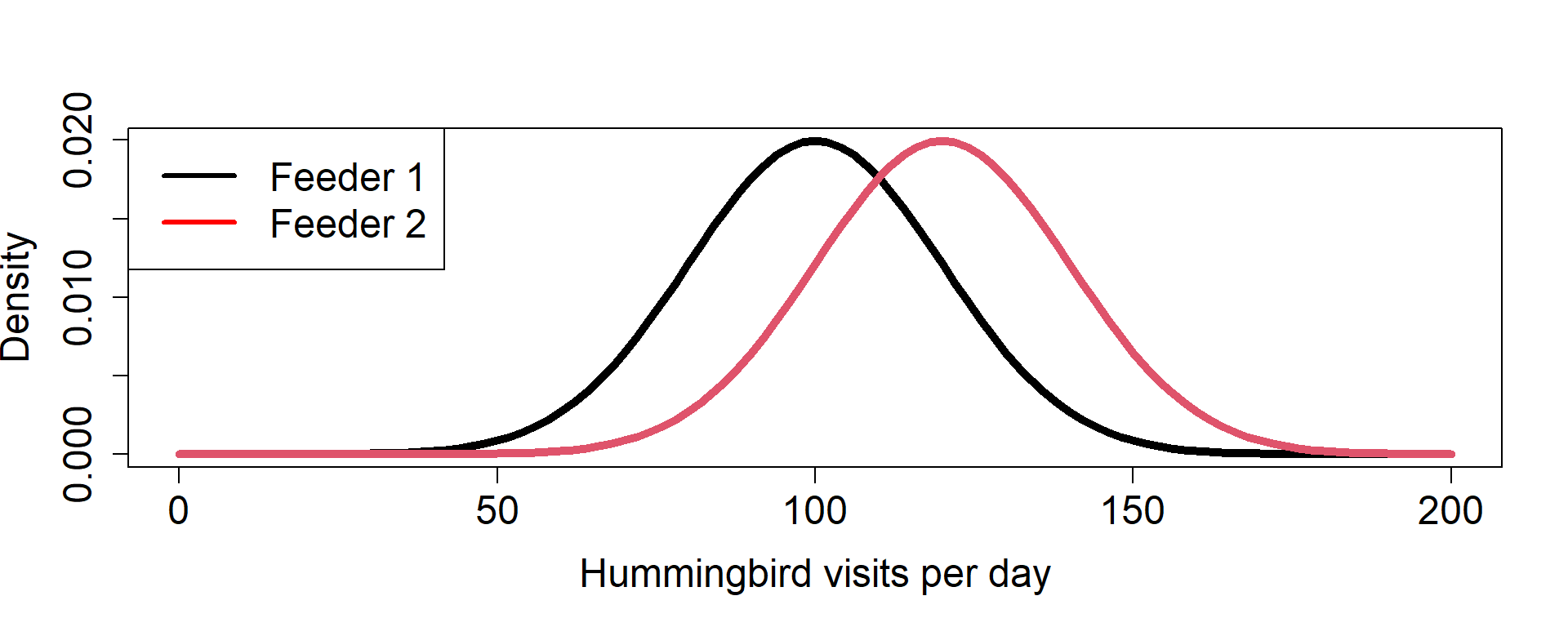
Case Study

Objective: To evaluate the relative use of two types of hummingbird feeders.

Case Study

Null Hypothesis
Mean daily use of each feeder is equal (\(\mu_{1} = \mu_{2}\)).

. . .

Alt. Hypothesis
Mean daily use of each feeder is not equal (\(\mu_{1} \neq \mu_{2}\)).

. . .

Statistical Test: two-tailed t-test

Case Study

First, we need to define TRUTH

  Group1.Mean <- 100
  Group1.SD <- 20
  
  Group2.Mean <- 120
  Group2.SD <- 20

. . .

Case Study (R Code)

library(pwr)
# Wish to test a difference b/w groups 1 and 2
# Want to know if there is a difference in means
 
#Difference in Means
  effect.size <- Group1.Mean-Group2.Mean

#Group st. dev
  group.sd <- sqrt(mean(c(Group1.SD^2,Group2.SD^2)))

#Mean difference divided by group stdev
#How does the numerator and denominator influence this number?  
  d <- effect.size/group.sd

Case Study

power = 0.8

out = pwr.t.test(d=d,power=power,type="two.sample",
                 alternative="two.sided")

#Sample Size Needed for each Group
out$n

[1] 16.71472

. . .

Assuming Independence b/w feeders
How do we design our sampling to ensure this?

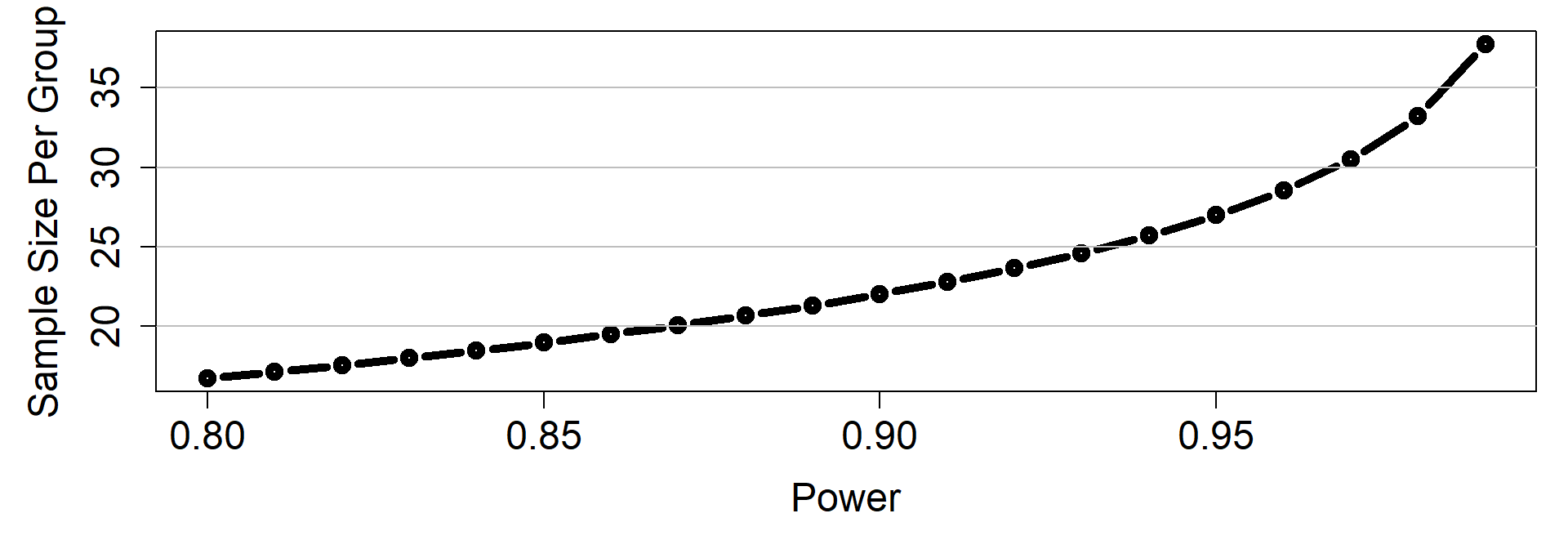
Tradeoff (Power vs N)

Let’s consider multiple levels of power

. . .

power = matrix(seq(0.8,0.99,by=0.01))

my.func = function(x){                    
                      pwr.t.test(d=d,power=x,
                                 type="two.sample",
                                 alternative="two.sided"
                                )$n
}

out= apply(power,1, FUN=my.func)

. . .

Truth?

These results assume we are correct about…

  Group1.Mean <- 100
  Group1.SD <- 20
  
  Group2.Mean <- 120
  Group2.SD <- 20

. . .

What if we are wrong?

How do we evaluate this?

Tradeoffs

Power, Effect Size, N

# Allow group 1 to vary
  Group1.Mean <- seq(10,110,by=5)

#THIS IS THE SAME
  Group1.SD <- 20
  Group2.Mean <- 120
  Group2.SD <- 20
  group.sd <- sqrt(mean(Group1.SD^2,Group2.SD^2))

# Variable effect.size  
  effect.size <- Group1.Mean-Group2.Mean
  d <- effect.size/group.sd

#setup combinations of d and power
  power = seq(0.8,0.99,by=0.01)
  power.d = expand.grid(power,d)
  power.d$Var1 = as.numeric(power.d$Var1)

. . .

#make new function and use mapply
my.func = function(x,x2){                    
                      pwr.t.test(d=x2,power=x,
                                 type="two.sample",
                                 alternative="two.sided"
                                )$n
}

# mapply function
  out= mapply(power.d$Var1,power.d$Var2, FUN=my.func)

# unstandardized the effect size back to difference of means
  power.d$Var2=power.d$Var2*group.sd
  
  out2=cbind(power.d,out)
  colnames(out2)=c("power","d","n")

Tradeoffs

Power, Effect Size, N