Simple Random Sampling

Goal

Goal: to know the mean number of boreal toad egg masses per pond in RMNP

  • different egg masses per pond is meaningful why?

SRS

Conceptual Walkthrough

  • We have a known population of ponds, N = 6

  • We have enough to money for n = 2

  • Will use SRS

Pond egg.mass
A 2
B 6
C 8
D 10
E 10
F 12

SRS

Population Parameters:

  • \(\mu = 8\)
  • \(N = 6\)
  • \(\sigma^2 = 12.8\)

SRS

How many possible unique samples are there (w/o replacement)

\[ {N}\choose{n} \]

. . .

\[ \frac{N!}{n!(N-n)!} \]

. . .

R

choose(6,2)
[1] 15

SRS

What is the probability of any one particular sample?


. . .

SRS: all samples have the same probability!


. . .

Convenient Sampling: What is the probability of one particular sample?

SRS

What is the probability pond “A” will be sampled”? Pond “B”?


. . .

Look at all possible combinations:

utils::combn(LETTERS[1:6],2)
     [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14]
[1,] "A"  "A"  "A"  "A"  "A"  "B"  "B"  "B"  "B"  "C"   "C"   "C"   "D"   "D"  
[2,] "B"  "C"  "D"  "E"  "F"  "C"  "D"  "E"  "F"  "D"   "E"   "F"   "E"   "F"  
     [,15]
[1,] "E"  
[2,] "F"

SRS

Sample.Number First Pond Second Pond First Value Second Value
1 A B 2 6
2 A C 2 8
3 A D 2 10
4 A E 2 10
5 A F 2 12
6 B C 6 8
7 B D 6 10
8 B E 6 10
9 B F 6 12
10 C D 8 10
11 C E 8 10
12 C F 8 12
13 D E 10 10
14 D F 10 12
15 E F 10 12

. . .

What is the probability pond “A” will be sampled”? Pond “B”?

SRS

Is it okay to not like your random sample and resample?

sample(LETTERS[1:6],2)
[1] "C" "F"

. . .

sample(LETTERS[1:6],2)
[1] "A" "B"

. . .

sample(LETTERS[1:6],2)
[1] "C" "D"

. . .

Yes, but why don’t you like it? Maybe SRS is not what you want.



SRS

Consider the sample mean \(\hat{\mu}\) for each sample

Sample.Number First Pond Second Pond First Value Second Value Sample.Mean Absolute.Deviation
1 A B 2 6 4 4
2 A C 2 8 5 3
3 A D 2 10 6 2
4 A E 2 10 6 2
5 A F 2 12 7 1
6 B C 6 8 7 1
7 B D 6 10 8 0
8 B E 6 10 8 0
9 B F 6 12 9 1
10 C D 8 10 9 1
11 C E 8 10 9 1
12 C F 8 12 10 2
13 D E 10 10 10 2
14 D F 10 12 11 3
15 E F 10 12 11 3

SRS

Sample.Number Sample.Mean Deviance.Truth
1 4 -4
2 5 -3
3 6 -2
4 6 -2
5 7 -1
6 7 -1
7 8 0
8 8 0
9 9 1
10 9 1
11 9 1
12 10 2
13 10 2
14 11 3
15 11 3

\[ \frac{1}{15}\times\sum_{i=1}^{15} (\hat{\mu}_{i}) = 8\]

\[\sum_{i=1}^N(\hat{\mu}_{i}-\mu) = 0 \]

Estimator Bias?

SRS

Sample.Mean Frequency Relative.Freq Mean.times.Rel.Freq
4 1 0.067 0.267
5 1 0.067 0.333
6 2 0.133 0.800
7 2 0.133 0.933
8 2 0.133 1.067
9 3 0.200 1.800
10 2 0.133 1.333
11 2 0.133 1.467
Sum 15 1.000 8.000

. . .

\[ E[\mu] = \sum_{q=1}^{Q} p_i \times \hat{\mu}_{i} = 8 \]

  • \(Q\) = number of unique sample means

  • \(p_i\) = probability of obtaining a given sample / relative frequency

SRS

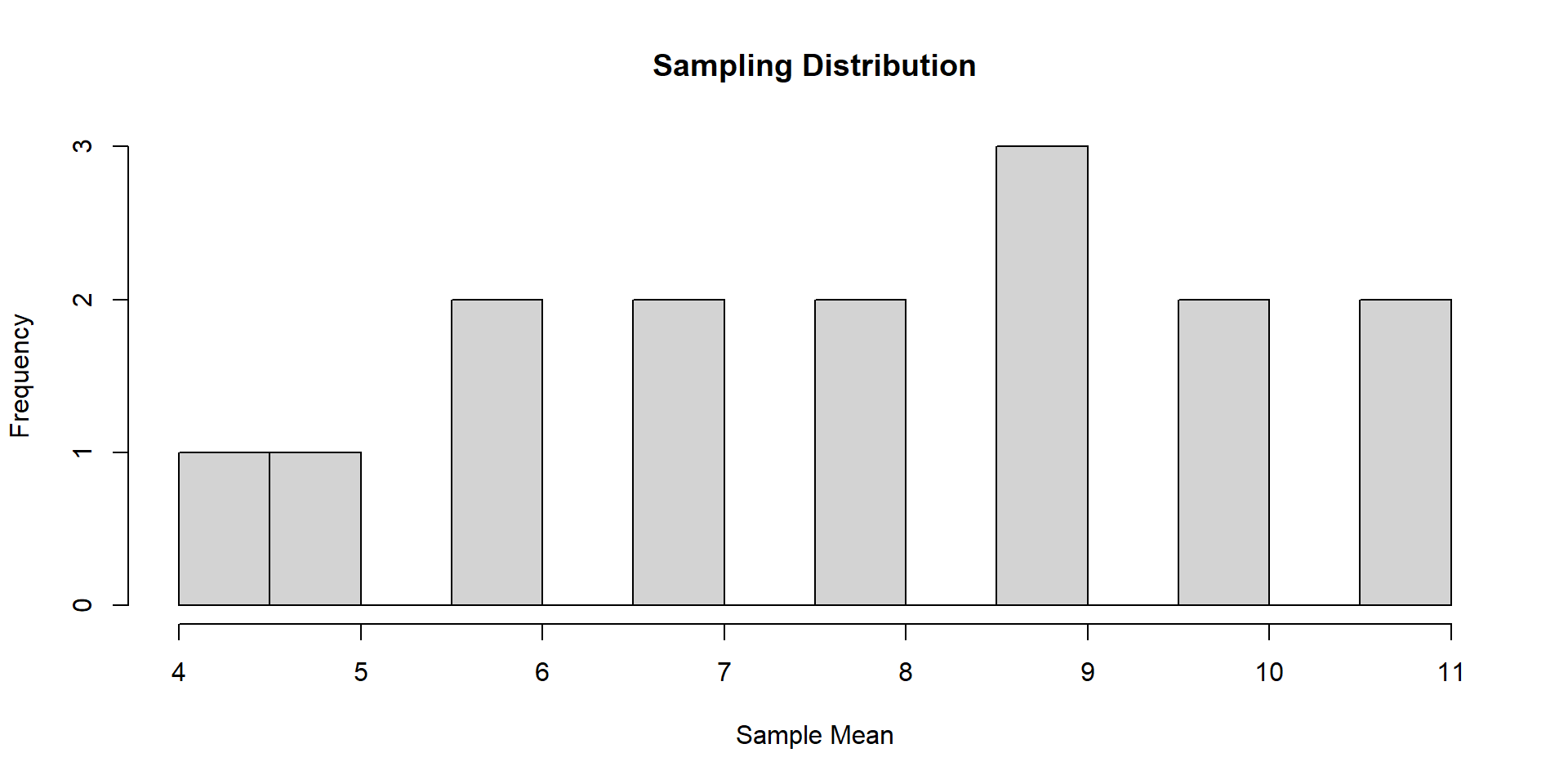
Sampling Disribution

  • Sample mean formula is an estimator of the population mean (parameter )
  • Sample mean is a random variable with a sampling distribution
    • sample mean varies from sample-to-sample becasue of the sampling process
  • The sampling distribution is specific to an estimator - has known outcomes and relative frequencies of values

Sampling Disribution

  • judge an estimator by its sampling distribution
  • What properties do we want?

Estimator Properties

  • Precise and unbiased estimator
  • Is our estimator precise?

Variance of Sampling Distribution

Sample.Number Sample.Mean Deviance.Truth
1 4 -4
2 5 -3
3 6 -2
4 6 -2
5 7 -1
6 7 -1
7 8 0
8 8 0
9 9 1
10 9 1
11 9 1
12 10 2
13 10 2
14 11 3
15 11 3 
var(ponds.simple$Sample.Mean)
[1] 4.571429

Population Variance

The variance of all sample units

\[ \sigma^{2} = \frac{1}{N-1}\sum_{i=1}^{N} \left(y_{i}-\mu\right)^{2} \]

\[ \sigma^{2} = \frac{1}{6-1}\sum_{i=1}^{6} \left(y_{i}-8\right)^{2} \]

(1/(6-1))*sum((ponds$egg.mass-8)^2)
[1] 12.8

Sample Variance

Estimate population variance from each sample

\[ \hat{\sigma}^{2} = \frac{1}{n-1}\sum_{i=1}^{n} \left(y_{i}-\hat{\mu}\right)^{2} \]

var.per.sample = apply(
                       cbind(ponds.all$`First Value`,ponds.all$`Second Value`),
                       1,
                       var
                       )
# Expected value of population variance
  mean(var.per.sample)
[1] 12.8

Sample Variance

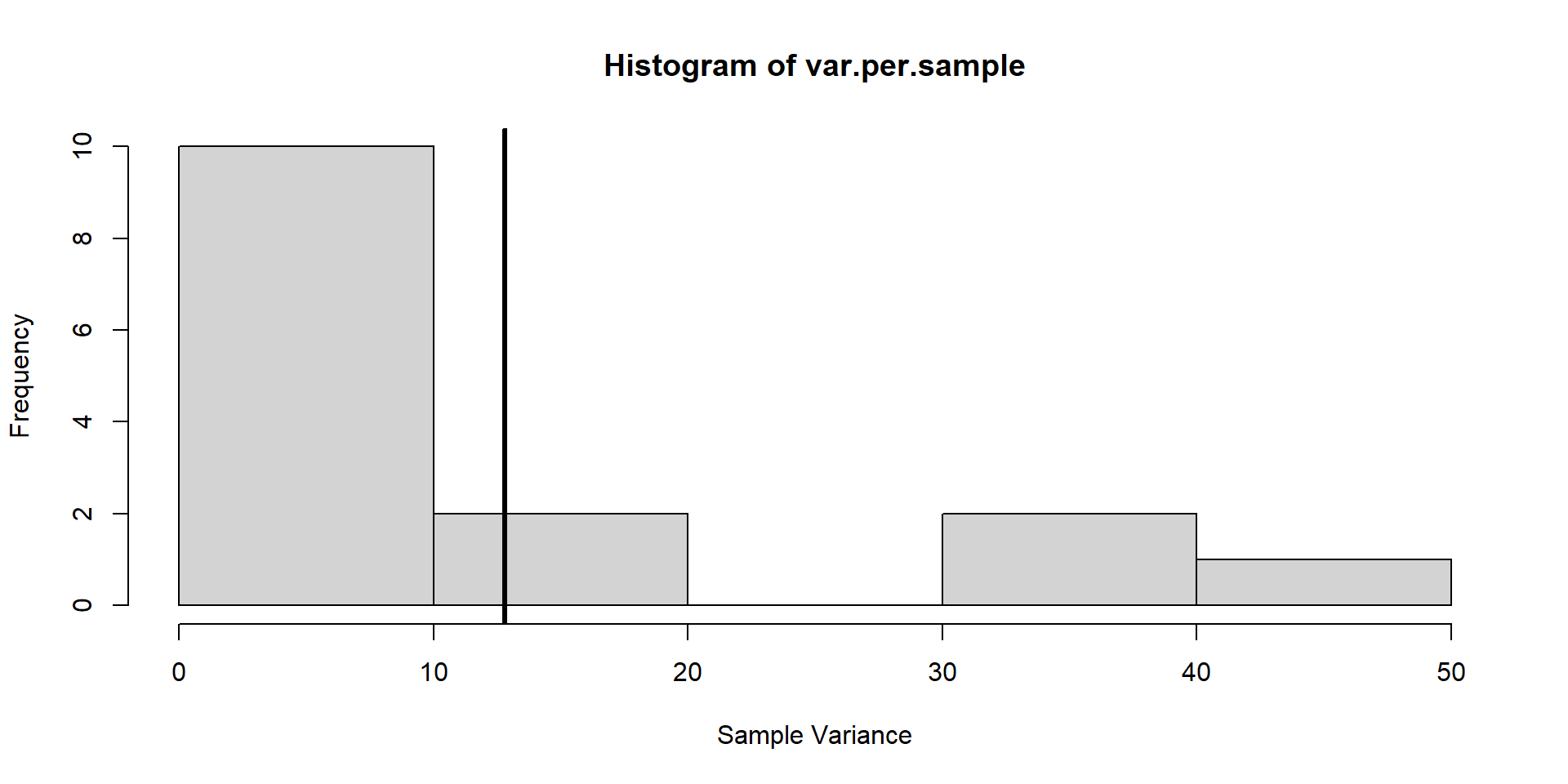
  • Unbiased estimate of the population variance.
  • Individual values will deviate from the population variance.

Connect these two

  • Population variance - variation among sample units; estimate from sample variance
  • Var. Sampling Distribution - variance of mean values from each possible sample

Connect these two

Variance of all units vs variance of all sample means

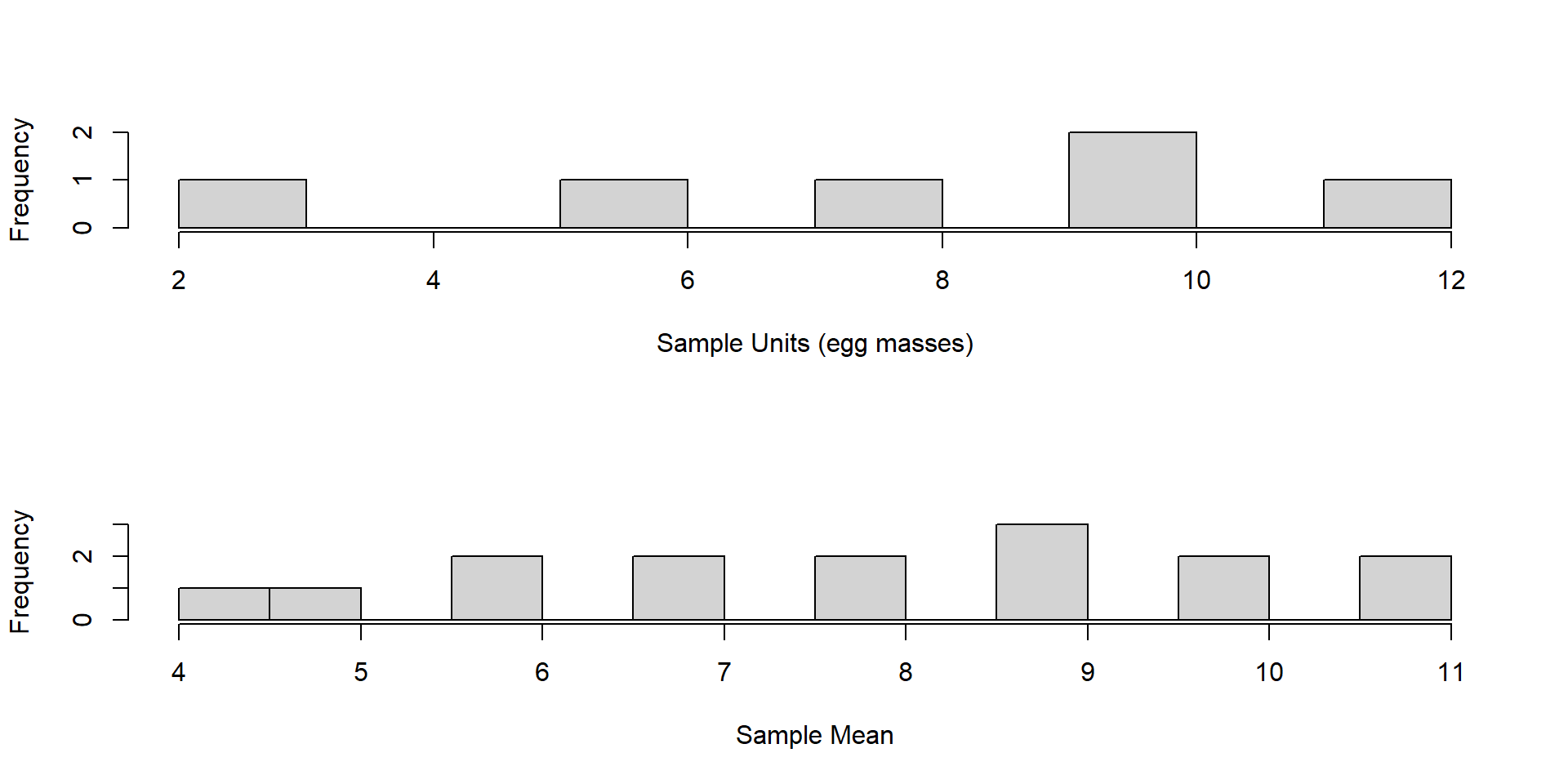
Connect these two

  • As the sample size (n) increases the sample variance declines by 1/n
  • Finite-population correction factor

\[ \left(\frac{N-n}{N}\right) \]

. . .

\[ E[\text{Sampling Distribution Variance}] = \frac{1}{n} \left(\frac{N-n}{N}\right) \times \text{Population Variance} \]

Connect these two

  • Sample size (n) = 2
  • Total units (N) = 6
  • E[pop var] = 12.8
  • E[sample dist. var] = 4.27
  • 1/n = 0.5
  • Finite correction factor = 0.67
  • E[pop var] \(\times\) 1/n \(\times\) FCF = 4.27

Connect these two

\[ E[\text{Sampling Distribution Variance}] = \\\frac{1}{n} \left(\frac{N-n}{N}\right) \times \text{Population Variance} \]

  • As n–> N, (N-n)/(N) approaches zero.
  • n = N then no sampling distribution variance
  • n << N then correction factor ~1 and expected sampling distribution variance is related to the population variance by 1/n

Connect these two

Why does this matter?

Connect these two

If you know the E[pop var] …

  • you have a mechanism to understand the variation of sample distribution of the means
  • the more variation in \(y\), the more variation in sampling dist. of means.

Sample Size

\[ E[\text{Sampling Distribution Variance}] \]

  • n = 2 –> 4.27
  • n = 3 –> 2.13
  • n = 4 –> 1.06
  • n = 5 –> 0.43
  • n = 6 –> 0

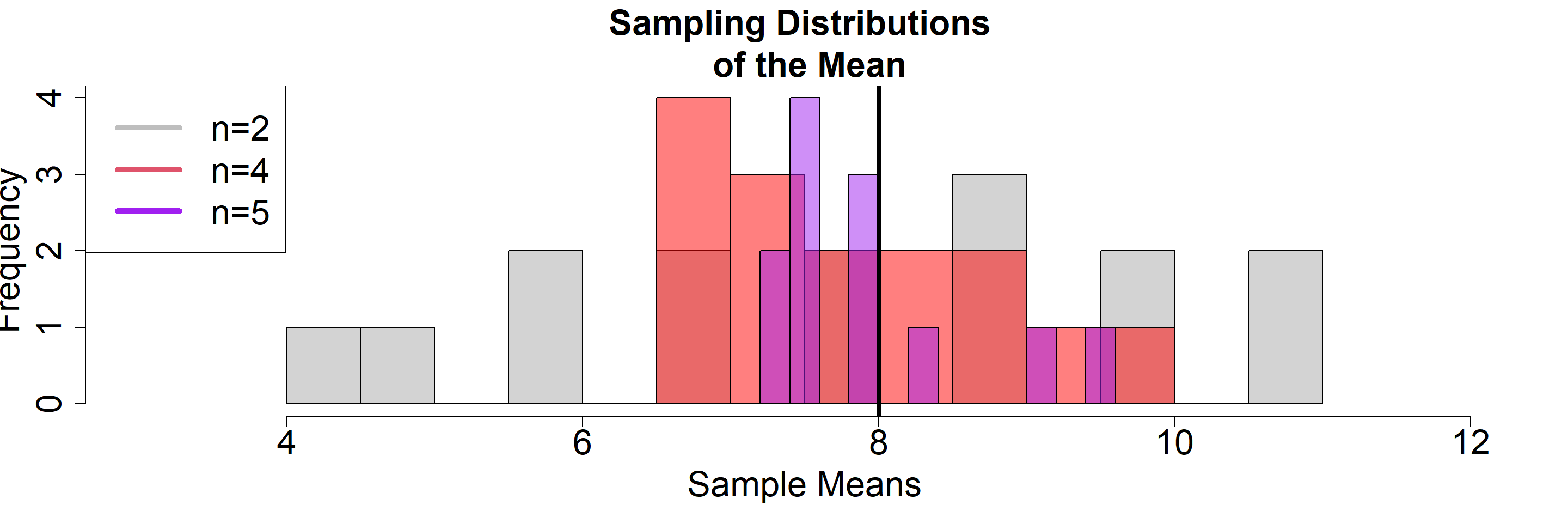
Sample Size

Not pond example; When N is large enough . . .

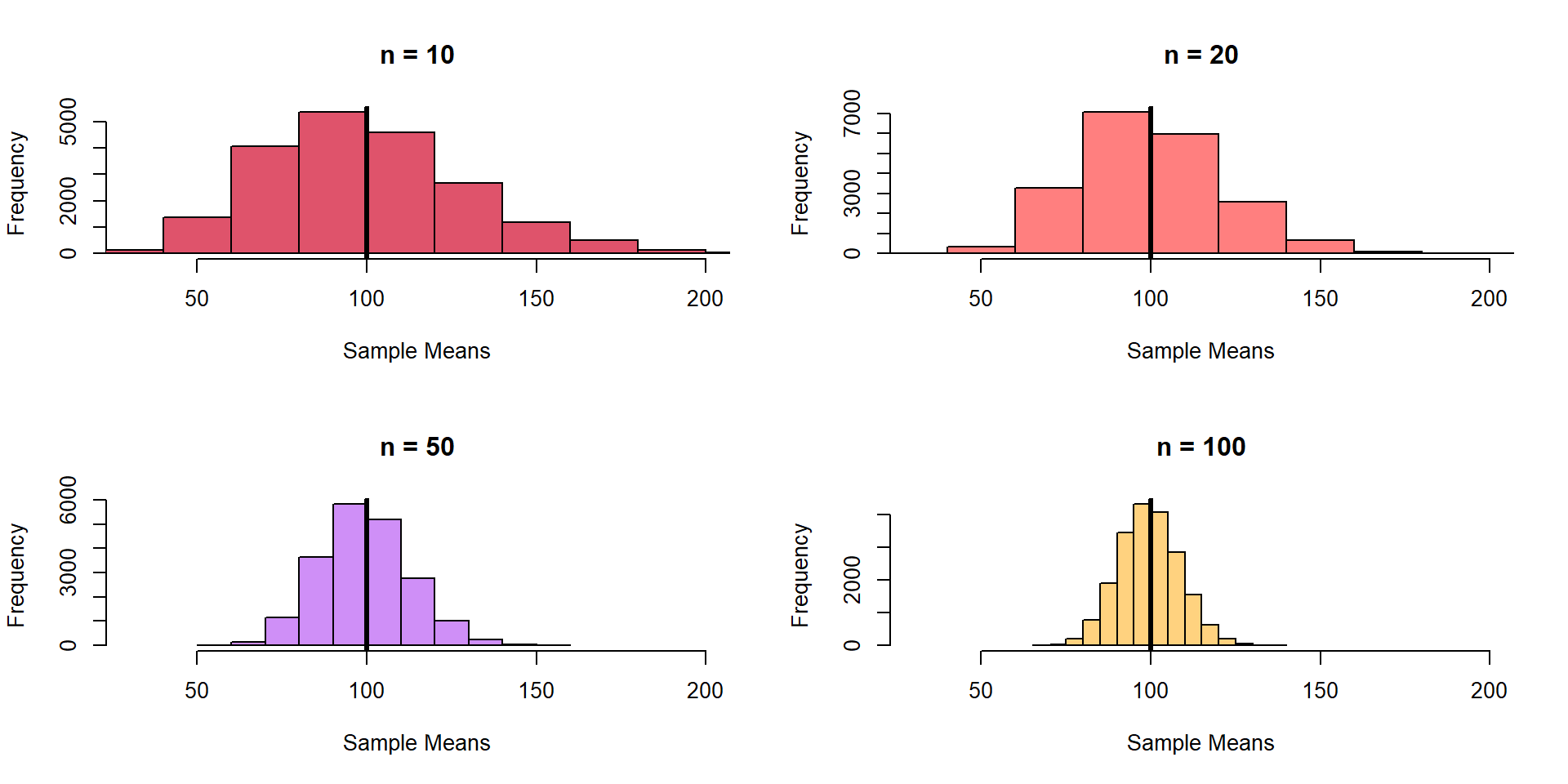
Sample Size

  • Sampling distribution is less variable
  • Sampling distribution centers on population mean
  • As n increases, the distribution becomes ‘Normal’

. . .

This is because of the Central limit theorem (CLT)

  • CLT relies on random/prob. based sampling
  • leads to parameter unbiasedness
  • Does not depend on distribution of samples
  • allows estimation of precision of parameters
  • allows estimation of confidence intervals

The TOTAL

Extrapolate the sample to the total population

\[ \hat{\tau} = N \times \hat{\mu} = \frac{N}{n}\sum_{i=1}^{n}(y_i) \]

The TOTAL

Back to ponds example

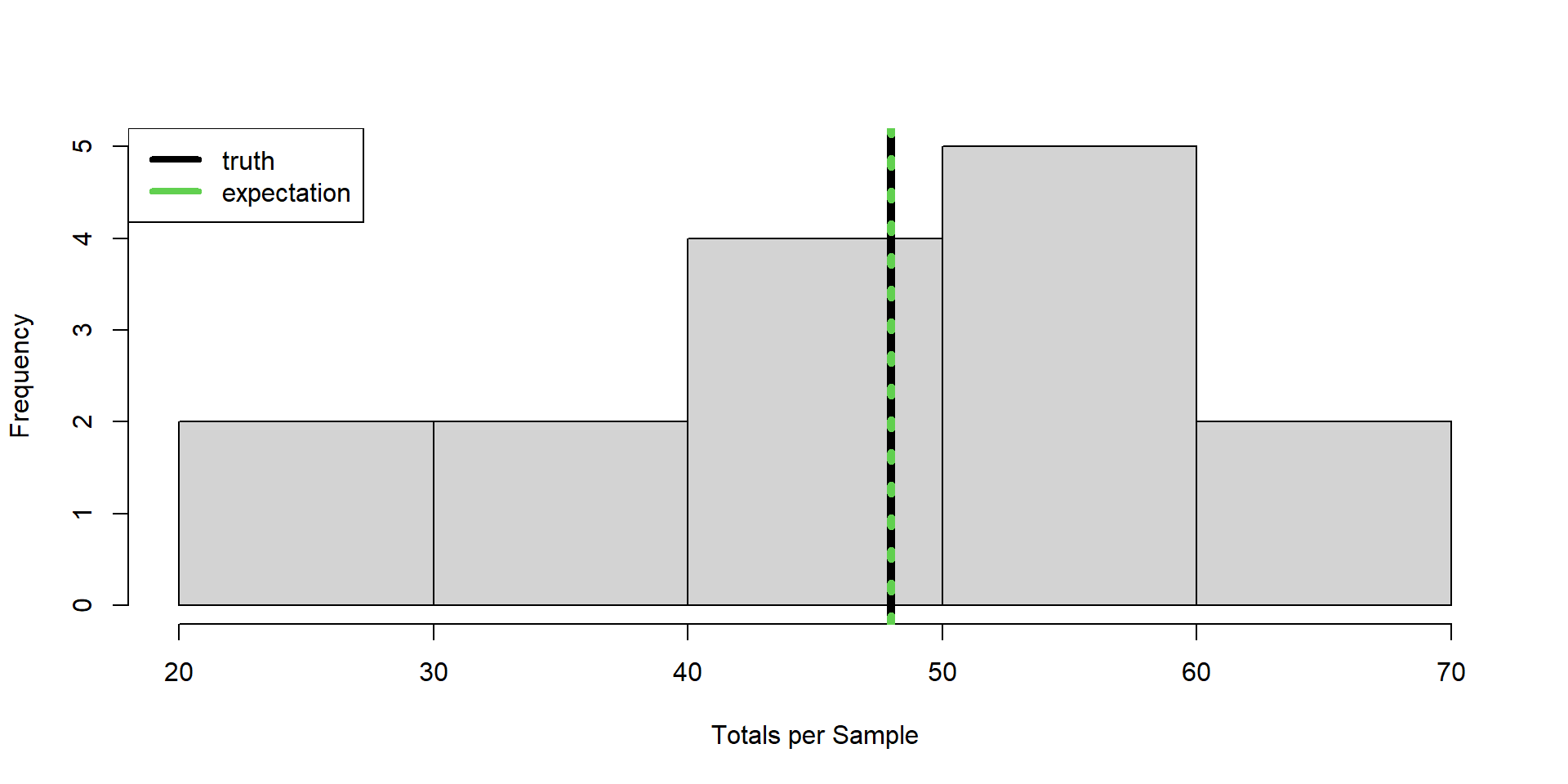
The TOTAL

Variance of the total

\[ \text{var}(\hat{\tau}) = N\times(N-1) \times \frac{\hat{\sigma}^2}{n} \]

Probabilty of

Whenever you have the sampling distribution, frame precision in terms of what matters to you.

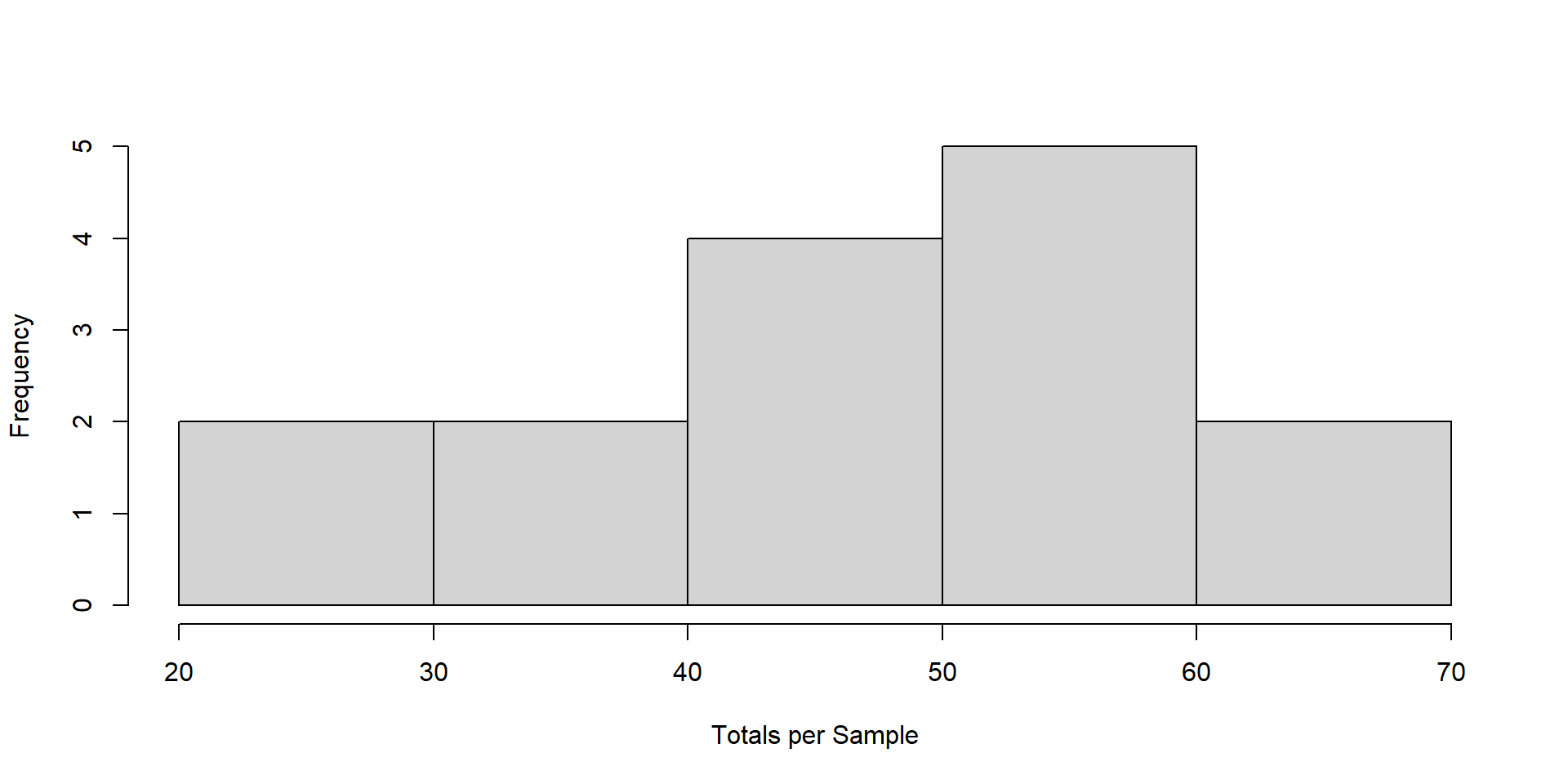
Probabilty of

\[ P(\hat{\tau}\leq 2 \times \tau) \]

length(which( tau.est <=  2*48))/length(tau.est)
[1] 1

Sample Size

But what \(n\)?

  • \(n\) impacts variation in estimates
  • variation in \(y\) impacts the influence of \(n\)
  • objective probably impacts \(n\) the most
  • higher \(n\) is not always better