Proportions

Strong Interest in fish/wildlife

Examples?

Proportions

\[ y \in \{0,1\} \]

\[ 1 = \text{occur} \\ 0 = \text{not occur} \]

\[ \hat{p} = \frac{1}{n}\sum_{i=1}^{n}y_{i} \]

\[ \hat{\sigma}^2_{p} = \left(\frac{N-n}{N}\right)\frac{\hat{p}(1-\hat{p})}{n-1} \]

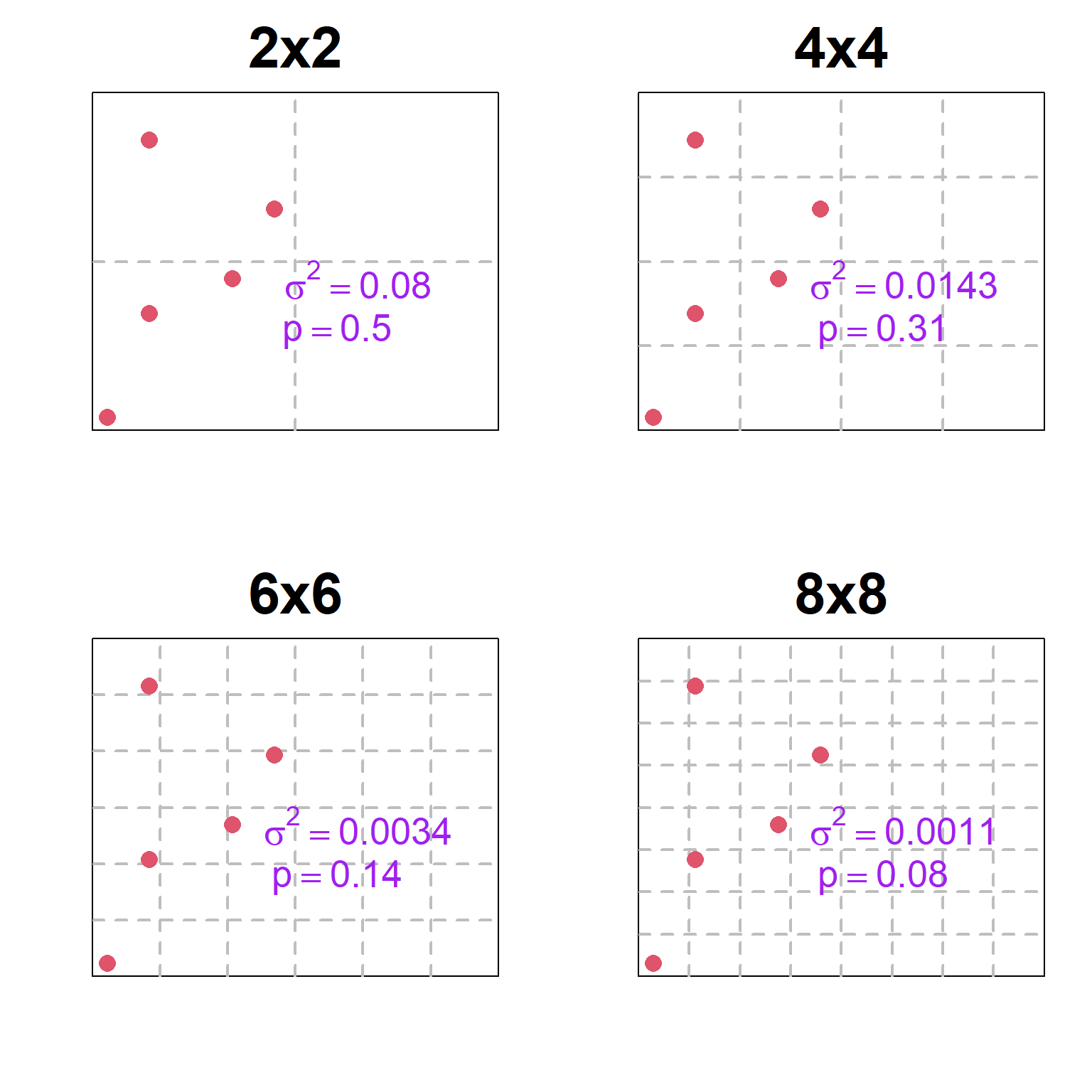
Proportion area occupied

How does sample grid effect \(\hat{p}\) and \(\hat{\sigma}^2_{p}\)?

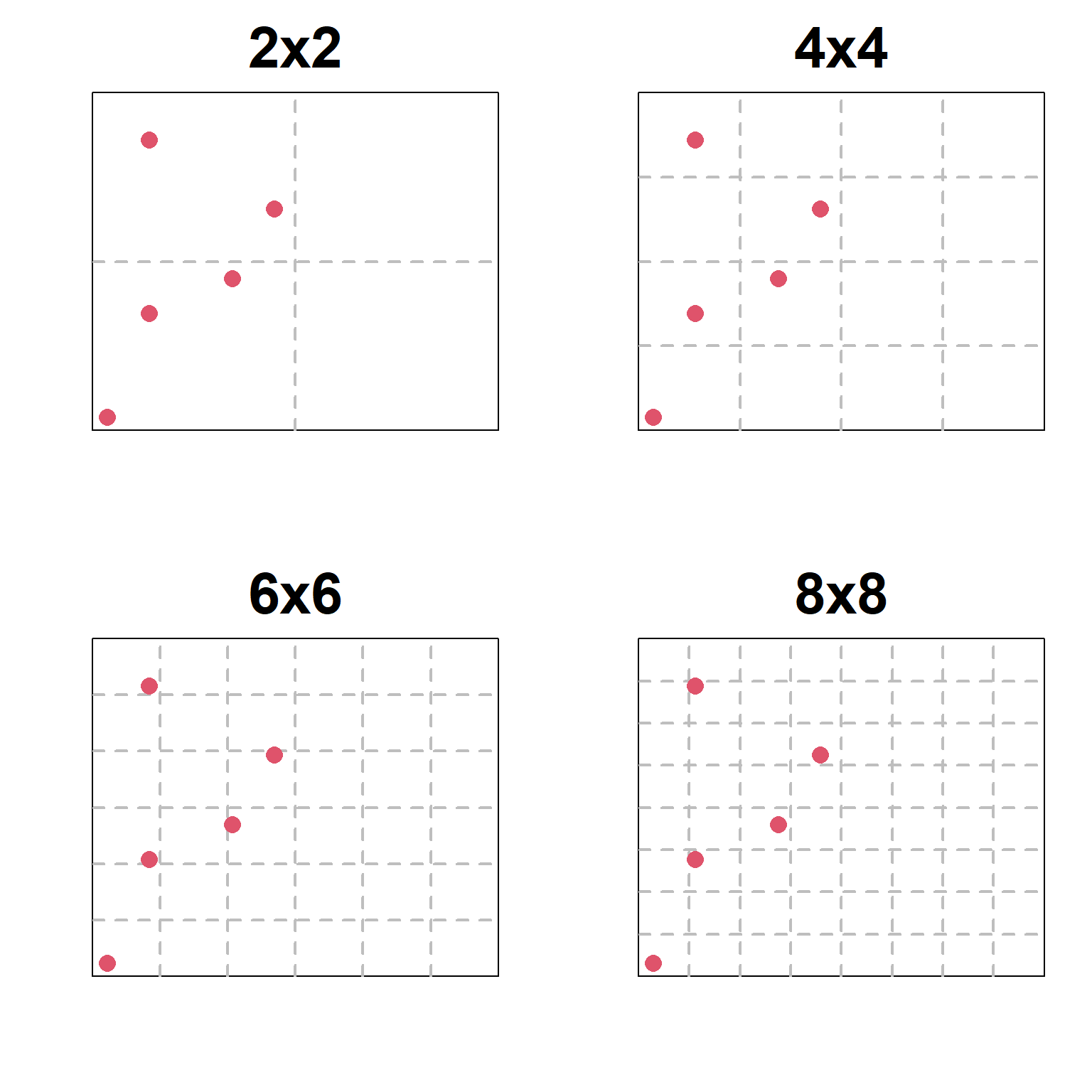
Proportion area occupied

How does sample grid effect \(\hat{p}\) and \(\hat{\sigma}^2_{p}\)?

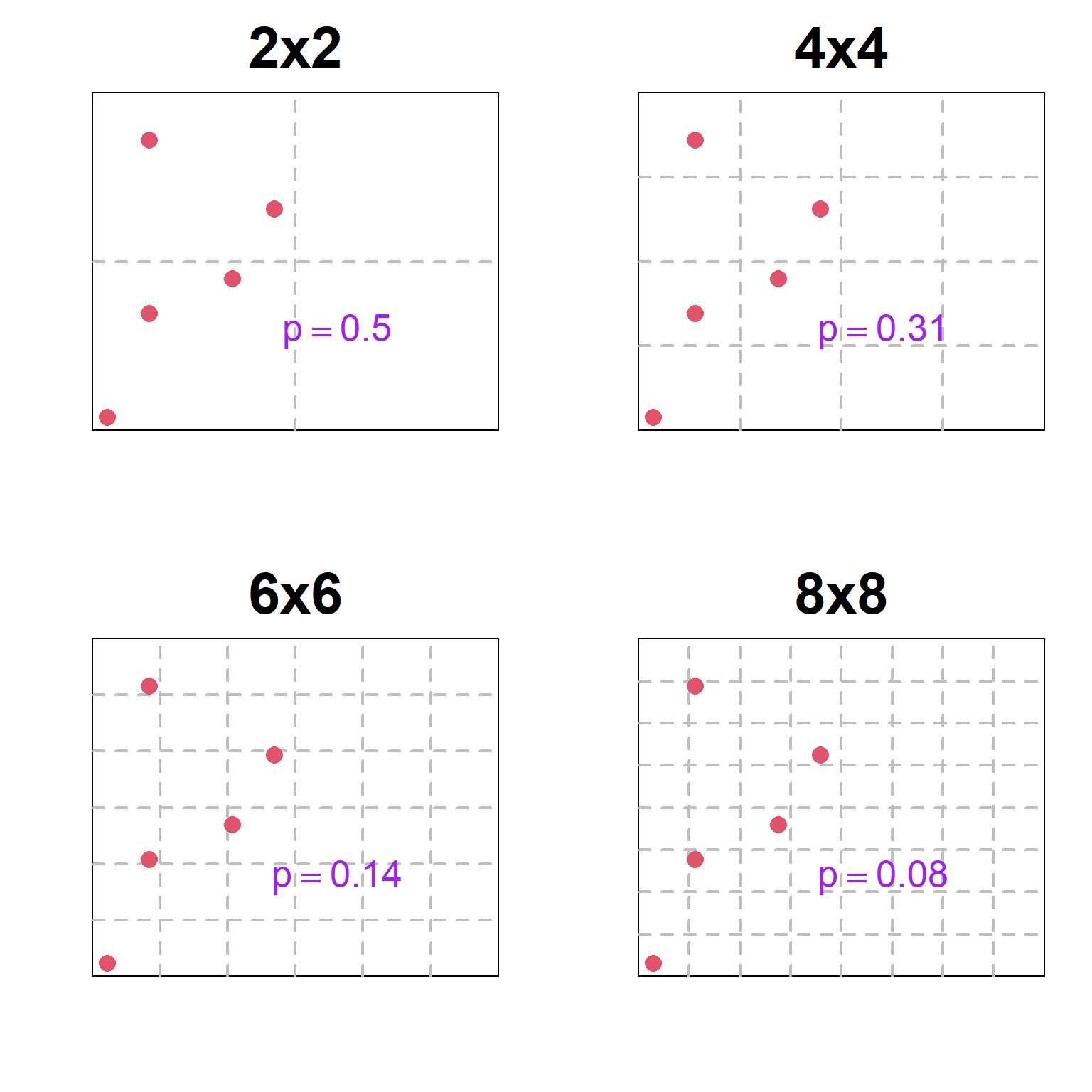
Proportion area occupied

How does sample grid effect \(\hat{p}\) and \(\hat{\sigma}^2_{p}\)?

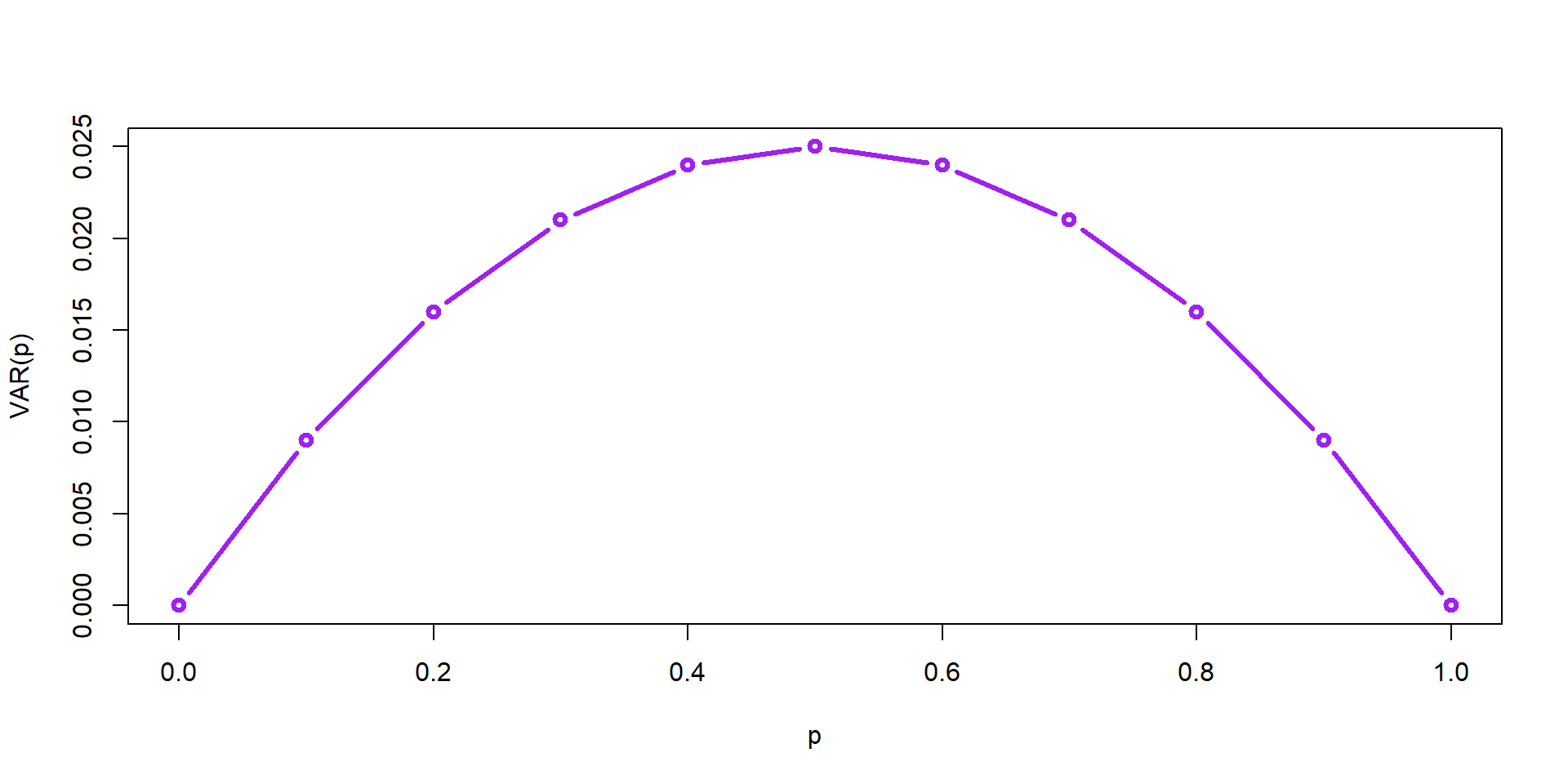
Var(p)

Does this make sense?

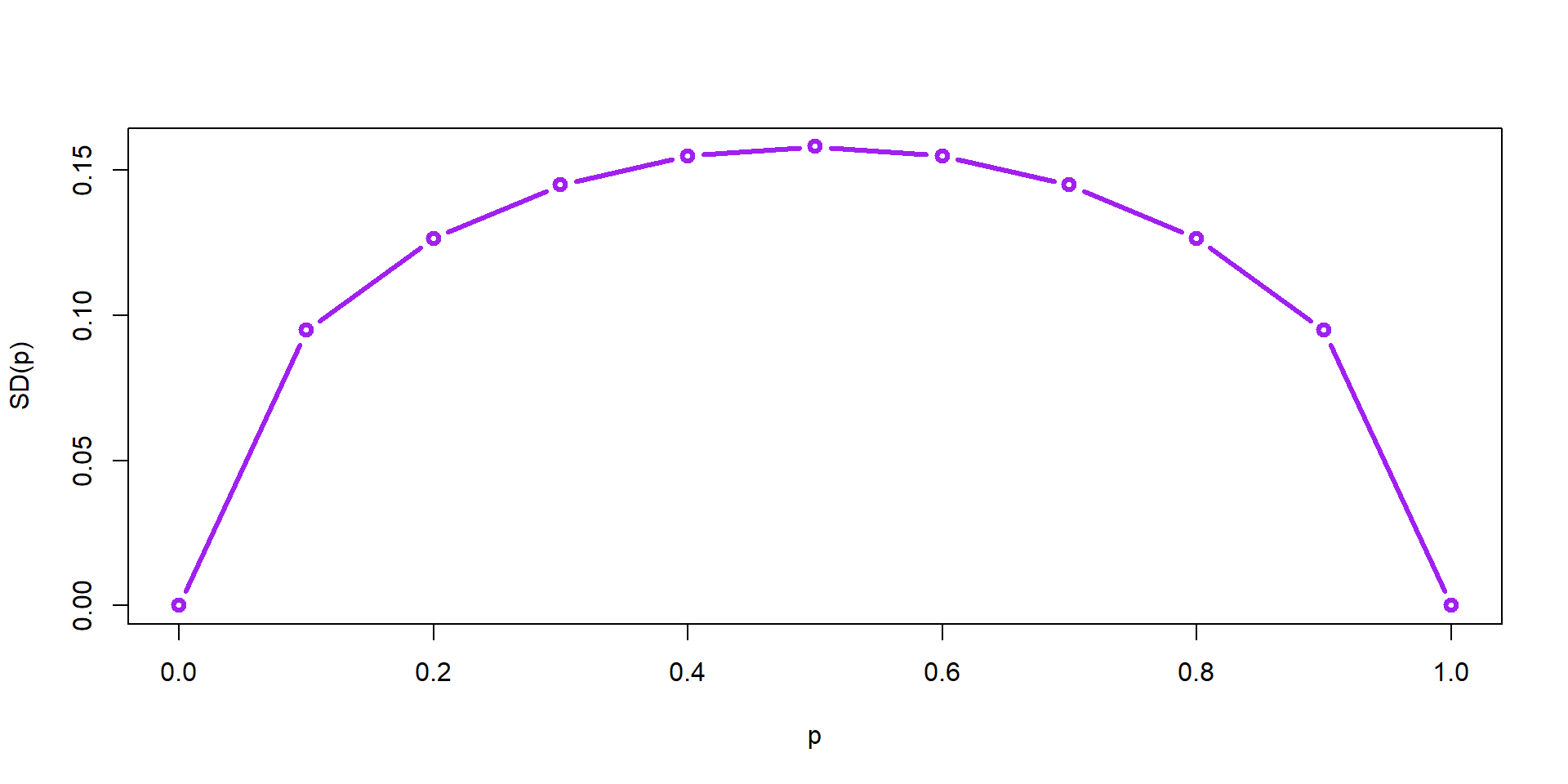
SD(p)

Soooooo useful!

\[ \hat{\sigma}_{p} = \sqrt\frac{\hat{p}(1-\hat{p})}{n-1} \]

how many fish should I tag?
how many elk should I track?
how many point intercepts should I take?
how many plots should I sample?

SD(p)

Lets visualize a few standard deviations of p

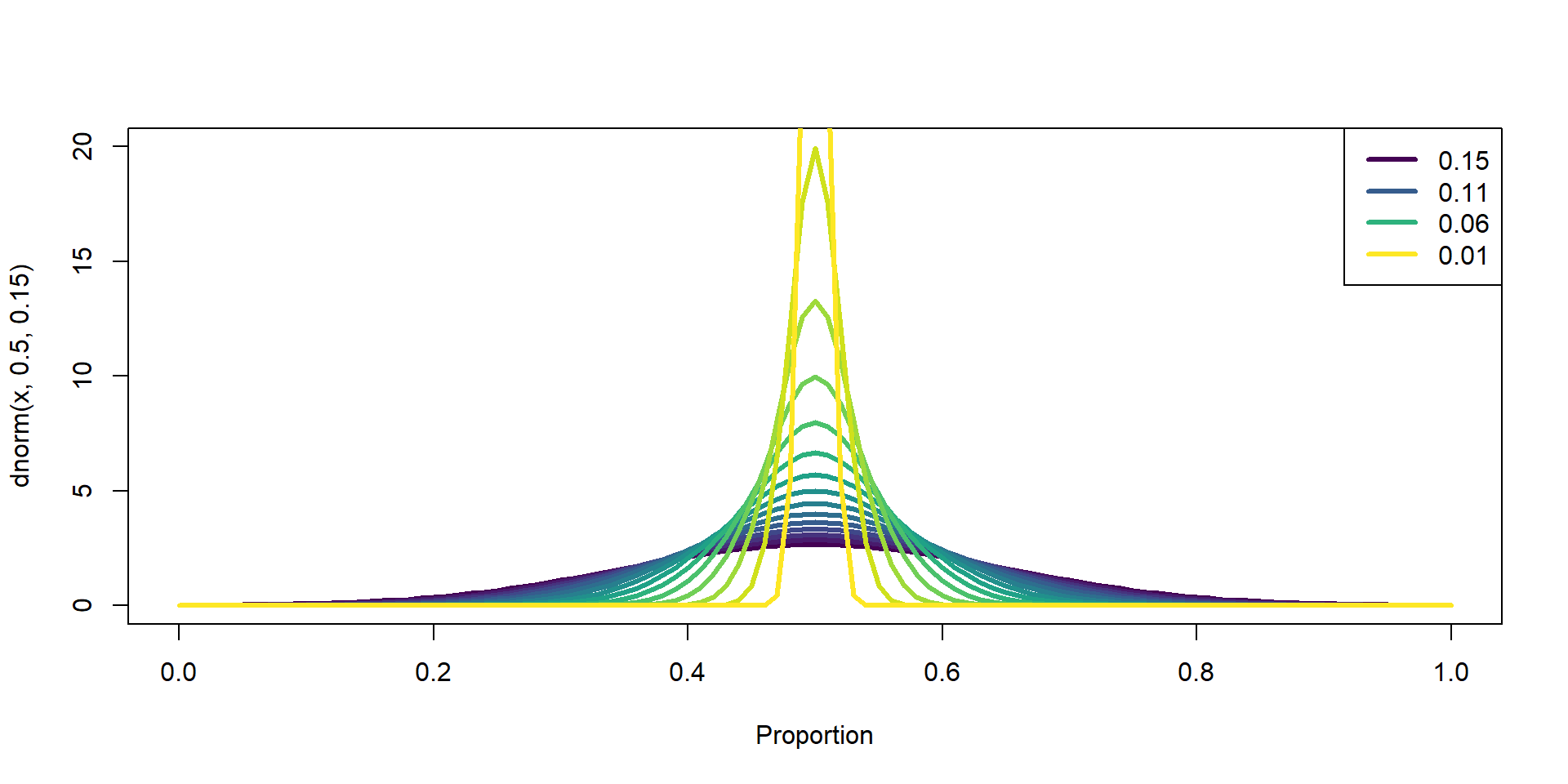
n, p, sd(p)

Wolverine Monitoring

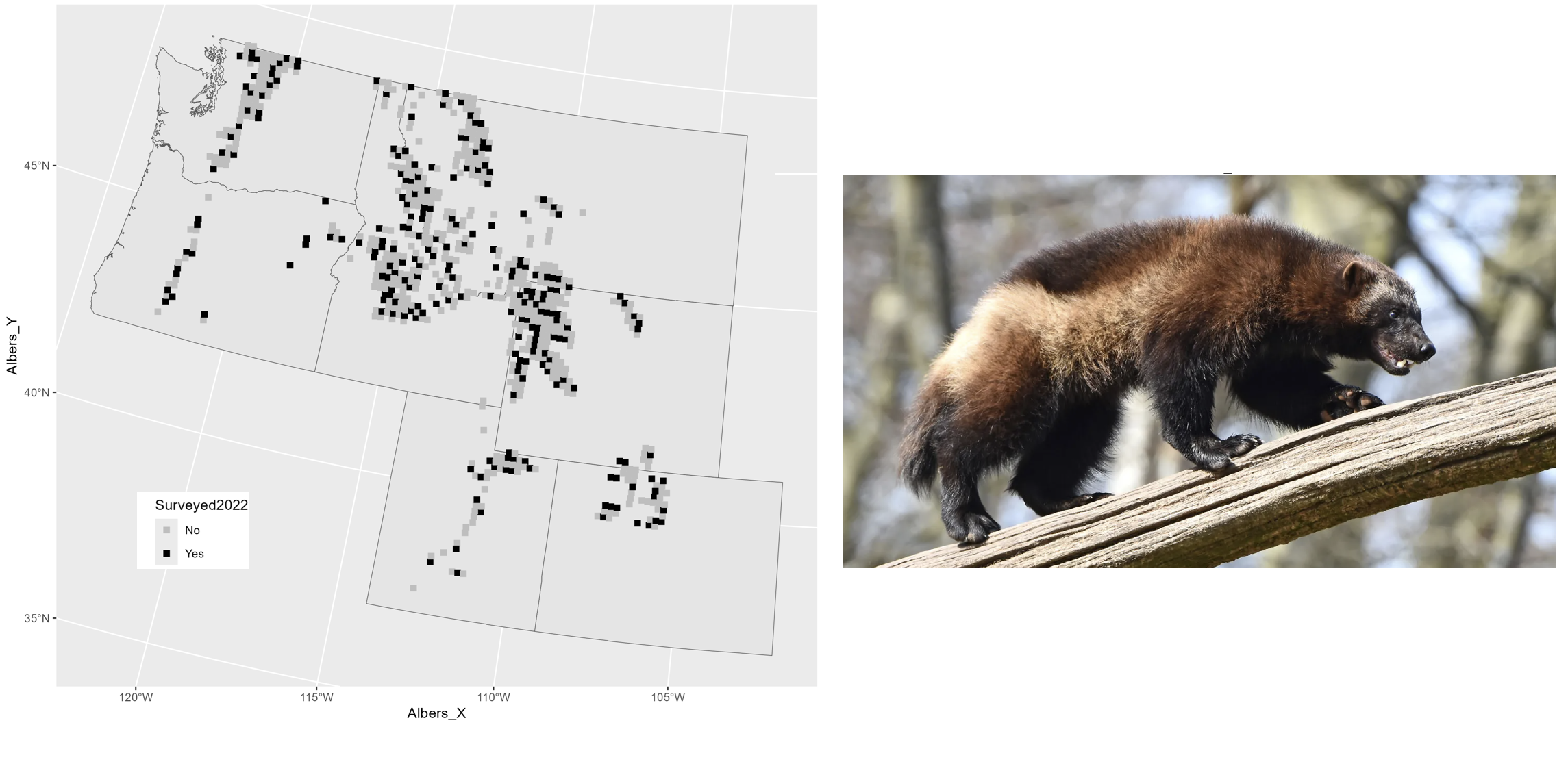
My Wolverine ‘Problem’

Sites surveyed by the States were selected via probabilistic sampling (GRTS)

a handful of additional sites were surveyed by other entities (e.g., NGO) using the same field protocol

Should I include the additional/ancillary surveys as data?

Should I report the cells with occurrences at all?

In small groups: Discuss and then tell me what to do and explain.

Simulation

What if?

N = 600
p = 0.5
SRS of n = 200

  sites occu
1     1    1
2     2    1
3     3    0
4     4    0
5     5    0
6     6    1

SRS

Sampling Distribution of \(\hat{p}\)

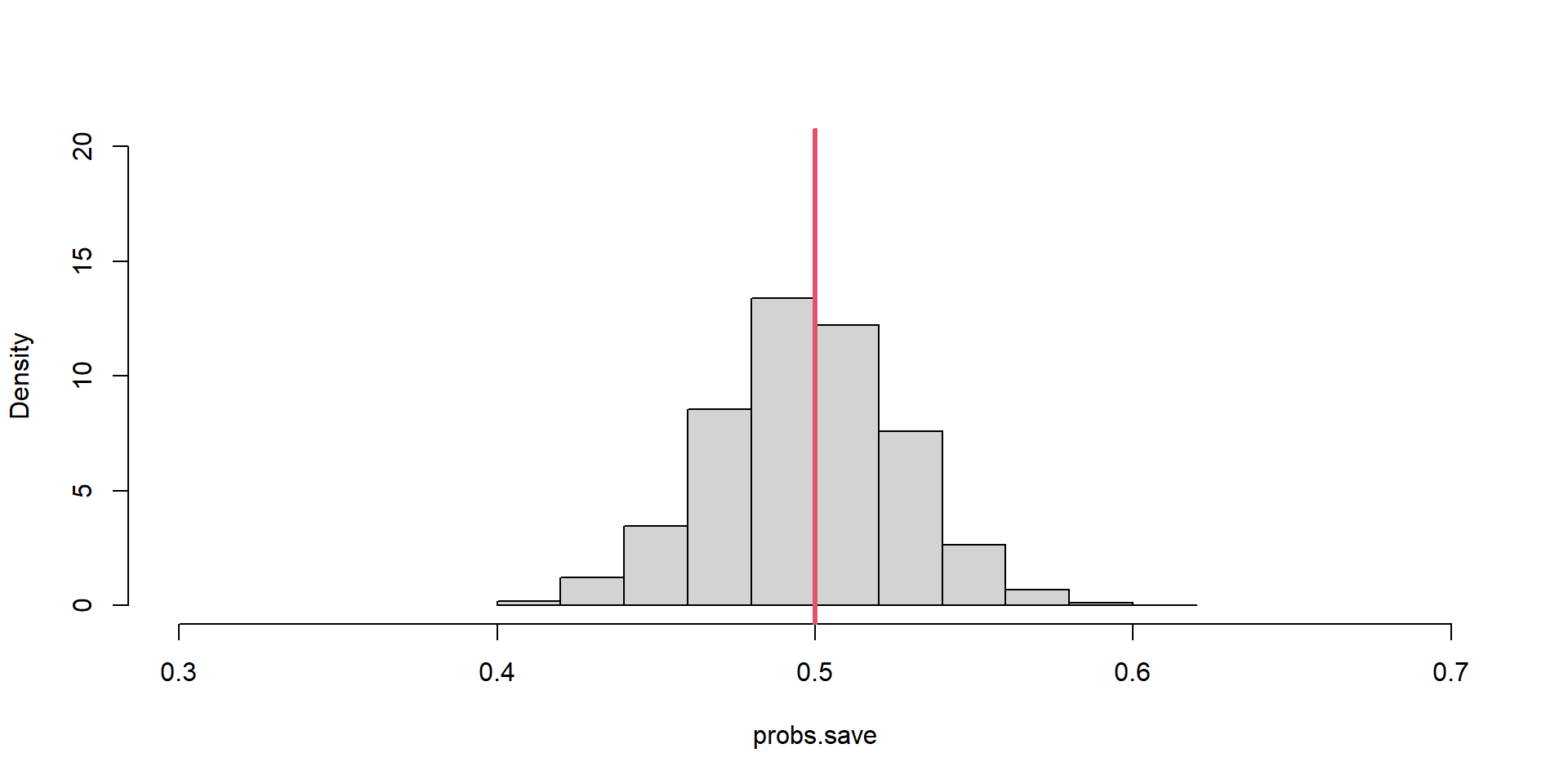
Estimator Bias = -0.00005
Distribution Var = 0.00084

Ancillary Occurences

SRS of n = 200 with 5% ancillary and occupied sites

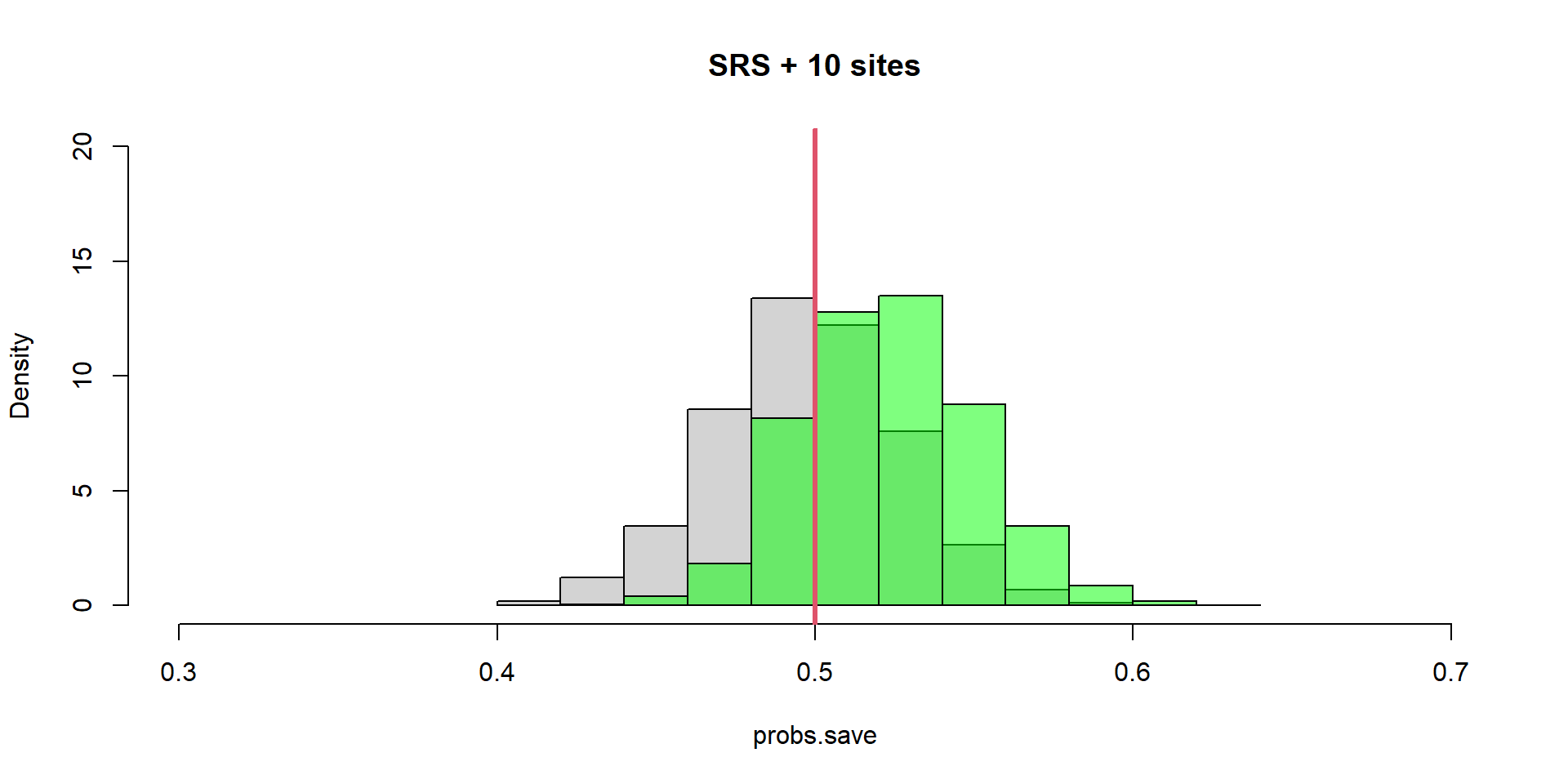
Estimator Bias = 0.02382
Distribution Var = 0.00073

Ancillary Occurences

SRS of n = 200 with 10% ancillary and occupied sites

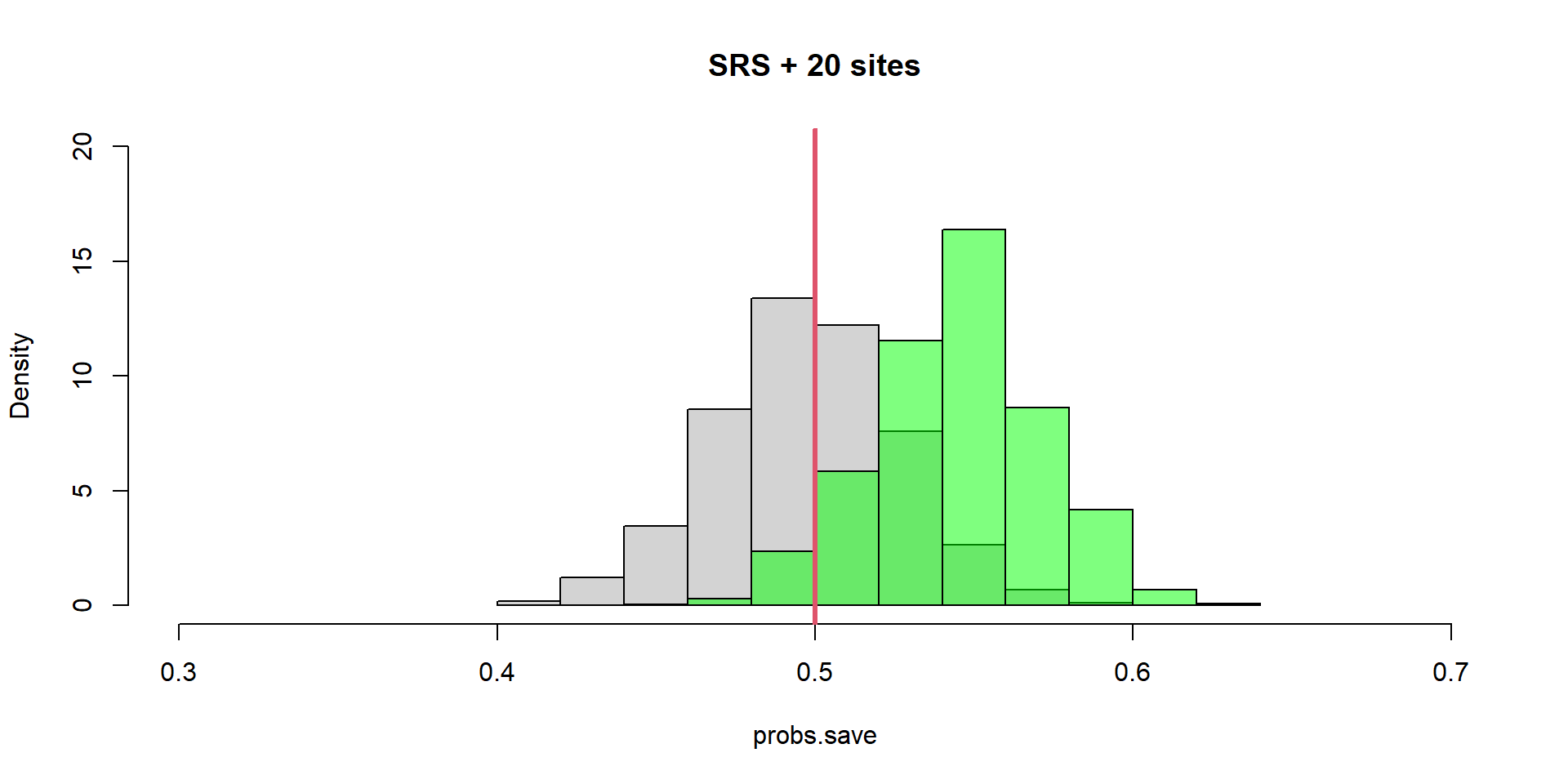
Estimator Bias = 0.04536
Distribution Var = 0.00069

My Wolverine ‘Problem’

Should I include the ancillary surveys as data?

Should I report the cells with occurrences at all?

My Wolverine ‘Problem’

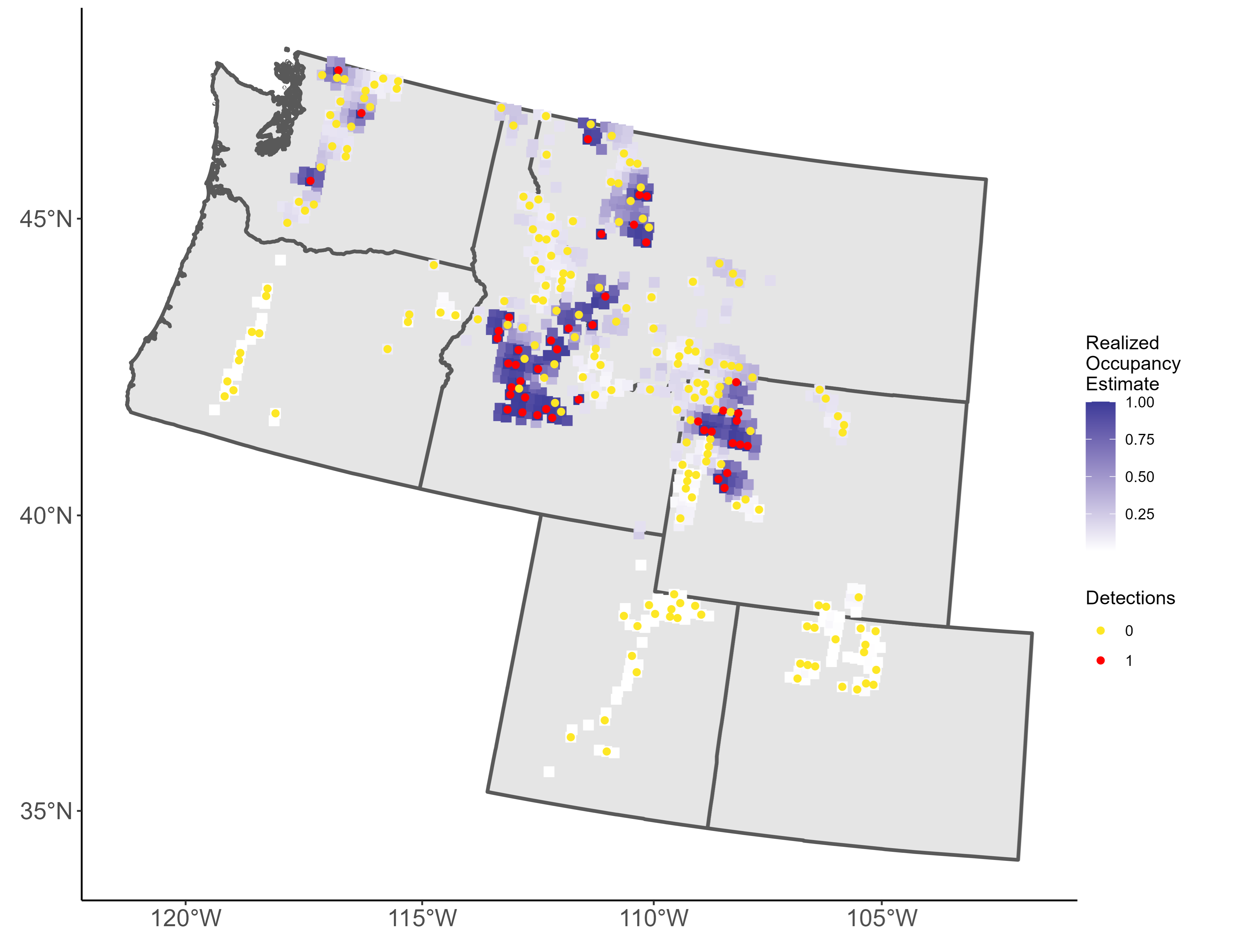
Unequal Probability of Sampling

Instead of adding sites w/o clear sampling probabilities, we make these explicit.

Identify sites that are important and increase their probability of being selected for sampling

Unequal Probability of Sampling

1/2 sites with 3x the probability of being sampled versus other half
sample function has an argument prob

\[ \hat{p} = \frac{1}{n}\sum_{i=1}^{n}y_i \]

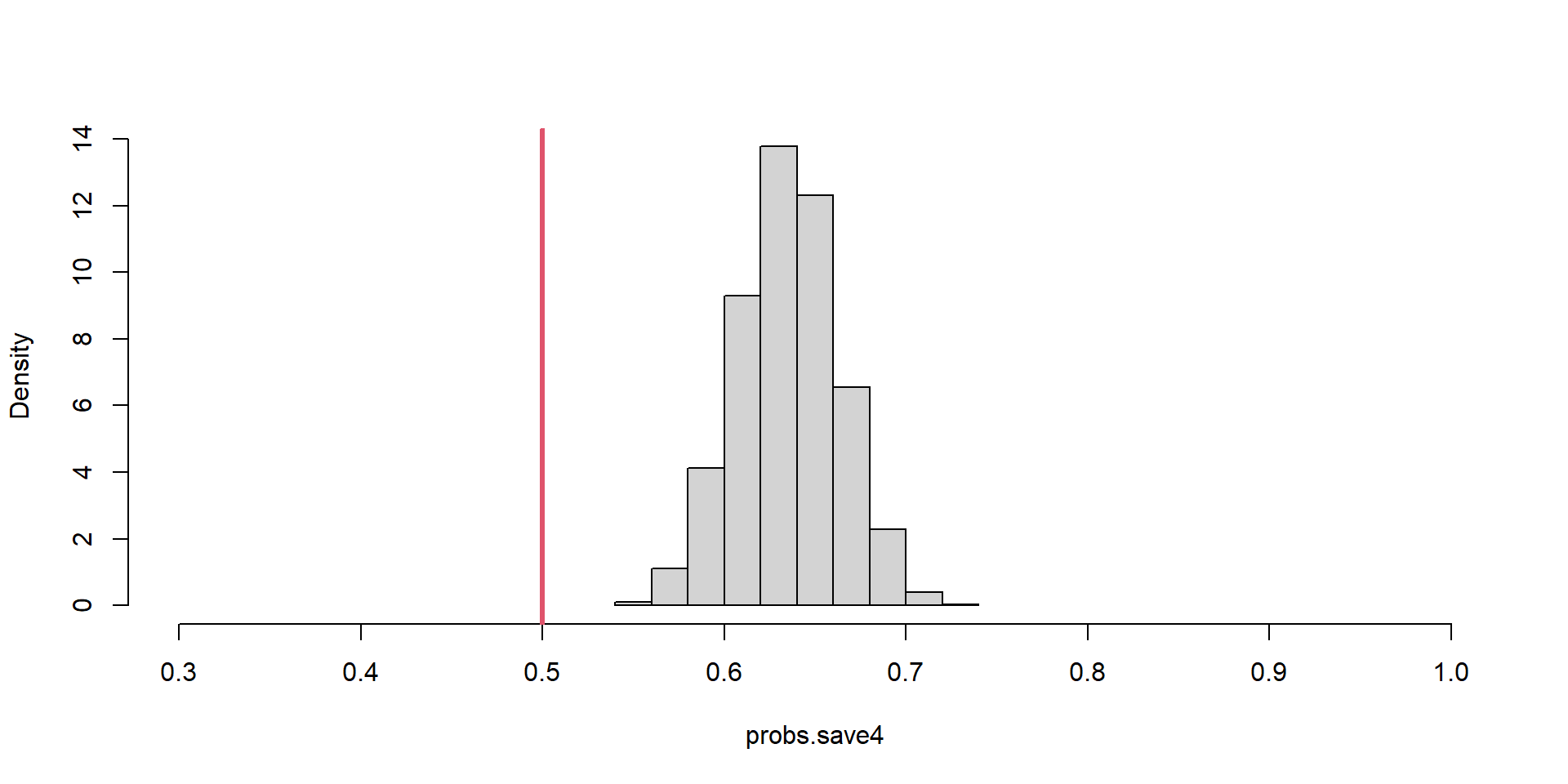
Estimator Bias = 0.13753

Unequal Probability of Sampling

Generalized Unequal Probability Estimator

Thompson Ch. 6.3

\[ \hat{\theta} = \frac{\sum_{i} y_i / \pi_i}{\sum_{i}1 / \pi_i} \]

\(\pi_{i}\) = probability of selecting sample \(i\).

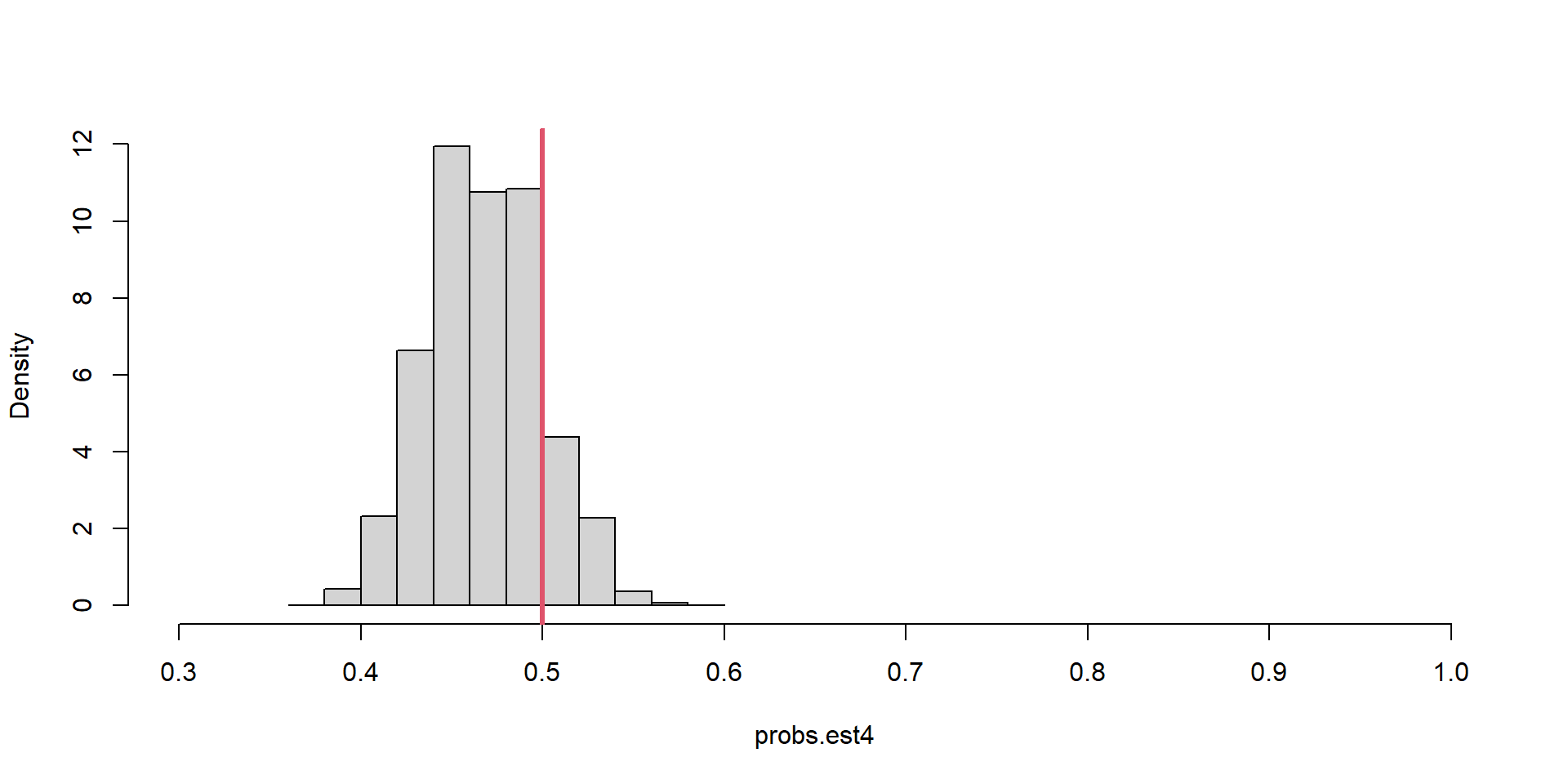
Estimator Bias = -0.03147

“not precisely unbiased” - Thompson