The Big Data Paradox



“era of big data” - what does this mean for our field?

Boyd et al. 2023

  • \(\sigma_Y\) is the population standard deviation
  • \(f = n/N\); sampling rate

“when \(\rho(R,Y) >0\): larger values of Y are more likely to be in the sample than in the population and vice versa. Where \(\rho(R,Y) =0\), this term cancels the others and there is no [systematic] error”.

Errors

  • Sampling Error is normal; big data or small data
  • The issue: correlation b/w obtaining an observation and the value of the observation (sample selection bias)
  • Survey data: correlation between whether a person responds and what their response is
  • Species distribution: correlation between where you sample and the probability the species occurs there

Big Data Paradox

Meng, X. L. (2018). Statistical paradises and paradoxes in big data (I): Law of large populations, big data paradox, and the 2016 US presidential election.


Bradley, V.C., Kuriwaki, S., Isakov, M. et al. Unrepresentative big surveys significantly overestimated US vaccine uptake.

Big Data Paradox

Three ways to reduce ‘errors’

\[ \begin{split} \text{errors} &= \begin{array} \normalfont{\text{data}} \\ \text{quality} \end{array} \times \begin{array} \normalfont{\text{problem}} \\ \text{difficulty} \end{array} \times \begin{array} \normalfont{\text{data}} \\ \text{quantitiy} \end{array} \end{split} \]

\[ \begin{split} \hat{\mu} - \mu &= \rho_{R,G} \times \sigma_{G} \times \sqrt(\frac{N - n}{n})\\ \end{split} \]

\(\rho_{R,G}\) is the data defect correlation between the true population values (G) and what is recorded (R); measures both the sign and degree of selection bias caused by the R-mechanism (such as non-response from voters from party X).

Big Data Paradox

\[ \begin{split} \hat{\mu} - \mu &= \rho_{R,G} \times \sigma_{G} \times \sqrt(\frac{N - n}{n})\\ \end{split} \]

Often assumed that Big data reduces errors by the magnitude of the data quantity


BUT, the nature of big data is such that \(\rho_{R,G} \neq 0\)

  • Major posit!

\(\rho_{R,G} = 0\) under simple random sampling (SRS)!

Big Data Paradox

Meng (2018) wanted to know the sample size (n) needed to achieve a certain level of error (mean squared error) with different levels of data quality:

  • \(\rho_{R,G} = 0\) (SRS) and
  • \(\rho_{R,G} = 0.005\) (Big Data))

  • The example was voter survey data for the 2016 U.S. presidential election.

  • the correlation between whether a person responds and what their response was

Back to Boyd et al. 2023

- \(f = n/N\)

  • When \(\rho_{R,G}\) deviates even slightly from 0, the relative effective sample size (\(n_{eff}/n\)) decreases with the true population size, N.(See Meng 2018; Figure 2)

Implication: When \(N\) is large, your relative ESS (\(n_{eff}/n\)) is small; your data are worthless.

“In biodiversity monitoring, N is typically very large, so this reduction can be substantial.”

Big Data Paradox

Look at big data for what it is

  • Meng’s voter survey example
    • n = 2,300,000
    • \(\rho_{R,G} = 0.005\)
    • \(N_{eff} = 400\) (assuming 100% response rate)
    • 0.99982608695 \(%\) reduction in sample size

Big Data Paradox

We need to think about Mean Squared Error (Proof)

\[ \text{MSE}(\hat{\mu}) = \frac{1}{n}\Sigma_{i=1}^{n}\left(\hat{\mu}_{i}-\mu\right)^{2} \]

\[ \text{MSE}(\hat{\mu}) = E[(\hat{\mu}-\mu)] \]

\[ \text{MSE}(\hat{\mu}) = \text{Var}(\hat{\mu})+(\text{Bias}(\hat{\mu},\mu))^{2} \]

Implication: Same MSE can be achieved with different combinations of variance and bias\(^2\).

Back to Boyd et al. 2023

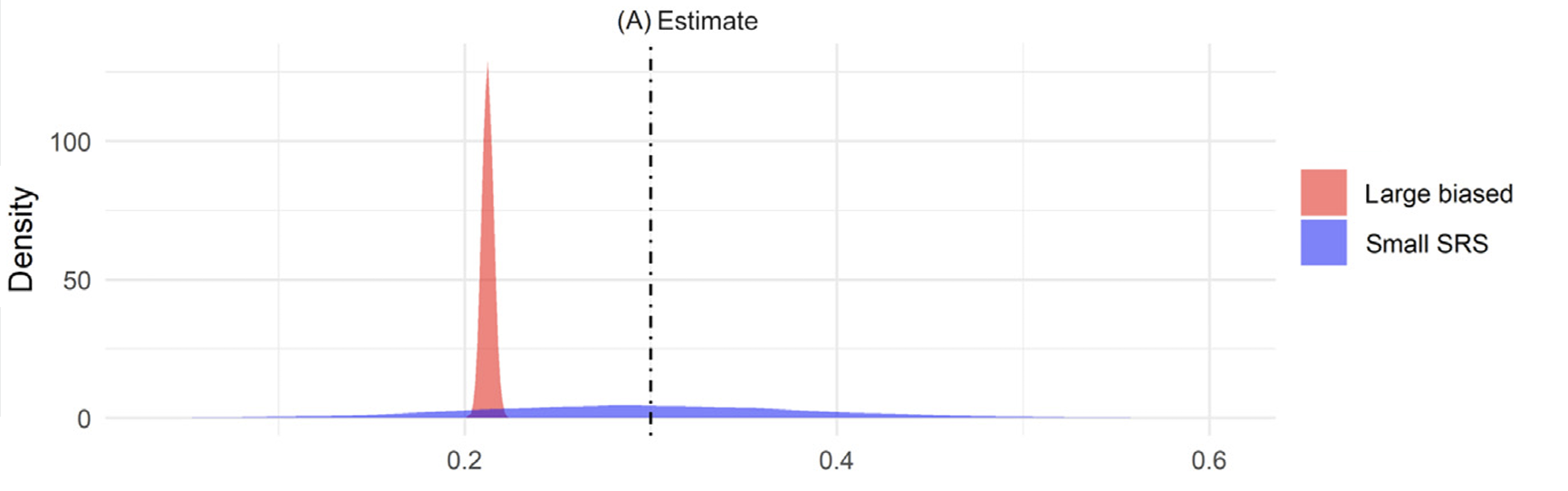
  • ‘large biased’ is \(\rho_{R,G} = -0.058\), \(n = 1000\)
  • MSE is the same
  • 95% CI’s include the truth 0% of the time for ‘Large Biased’

Back to Boyd et al. 2023

Take home: Large biased data –> highly biased and highly precise estimates

Meng (2018)

  • “…what should be unbelievable is the magical power of probabilistic sampling, which we all have taken for granted for too long.”
  • “once we lose control over the \(R\) mechanism, we can no longer keep the monster \(N\) at bay, so to speak.”
  • “It is therefore essentially wishful thinking to rely on the “bigness” of Big Data to protect us from its questionable quality, especially for large populations.”

Big Data Paradox

Is there really a choice?

  1. Big Data with sample selection bias

  2. Small sample from Simple random sample (no selection bias)